Поглощение света за счет оптических переходов электронов из состояний в валентной зоне в состояния зоны проводимости называется межзонным или собственным. Этот вид поглощения в полупроводниках является наиболее сильным и важным с точки зрения использования в различных приборах оптоэлектроники.

В случае изолированных КЯ волновые функции начального и конечного состояний электронов при межзонном поглощении с учетом (2.3) имеют следующий вид:

,

(4.10)

,

(4.11)

где и – периодические части волновых функций Блоха, соответствующих потолку валентной зоны и дну зоны проводимости объемного полупроводника, из которого состоит КЯ. Собственные значения энергии этих функций, отсчитанные от дна зоны проводимости и потолка валентной зоны, с учетом (2.8) равны

,

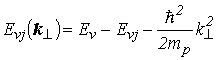(4.12)

.

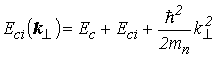(4.13)

Матричный элемент импульса (4.6) с учетом вида функций (4.10), (4.11) равняется

,

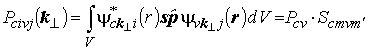(4.14)

где

,

(4.15)

– матричный элемент проекции оператора импульса на световой вектор, определяющий вероятность межзонного оптического перехода в области края собственного поглощения объемного прямозонного полупроводника, из которого состоит КЯ; - объем элементарной ячейки этого полупроводника;

(4.16)

– интеграл перекрытия огибающих функций, определяющий дополнительные правила отбора для вероятности межзонного оптического перехода между подзонами одномерной КЯ; L – эффективная ширина КЯ с учетом туннелирования электронов в потенциальные барьеры (ПБ). В приближении бесконечно глубоких КЯ с учетом формул для огибающих (2.5) интеграл перекрытия принимает два возможных значения:

.

(4.17)

Из формулы (4.17) следует, что межзонное оптическое поглощение в рассматриваемом случае имеет место только между подзонами с одним и тем же номером. В случае КЯ конечной высоты за счет туннелирования электронов в барьеры возможным становится поглощение, связанное с переходами между подзонами разного номера, но одной и той же четности. Однако интенсивность этого поглощения будет намного слабее, чем поглощение между подзонами с одним и тем же номером.

С учетом вышеприведенных формул (4.7) – (4.17) выражение для коэффициента поглощения света в КЯ в области края собственного поглощения принимает следующий вид:

,

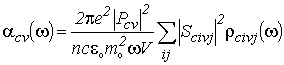(4.18)

где – функция оптической плотности (4.8), равная

,

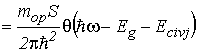(4.19)

где – ширина запрещенной зоны объемного полупроводника; ; – оптическая эффективная масса или эффективная масса оптической плотности состояний

.

(4.20)

Как указывалось ранее, зависимость функции оптической плотности совпадает с зависимостью плотности состояний от энергии в отдельных подзонах разрешенных зон (см. (3.6)).

С учетом (4.19) формула (4.18) принимает следующий вид:

,

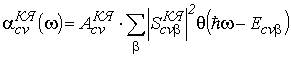(4.21)

где ; – совокупность квантовых чисел, соответствующих подзоне валентной зоны с номером j и подзоне зоны проводимости с номером i;

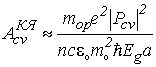(4.22)

– константа, значение которой определяется параметрами объемного полупроводника, из которого состоит КЯ, и шириной квантовой ямы ; – интеграл перекрытия волновых функций, определяемый формулой (4.16) или (4.17).

Согласно теории Кейна для энергетического спектра алмазоподобных прямозонных полупроводников А³В⁵ с решеткой цинковой обманки модуль матричного элемента импульса связан с шириной запрещенной зоны формулой

.

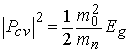С учетом этой формулы константа (4.22) для КЯ из рассматриваемых полупроводников будет равняться

 

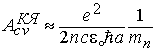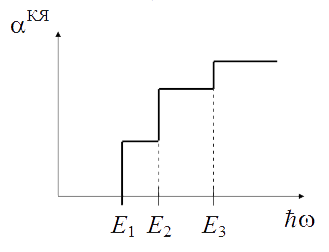
Согласно формуле (4.21) край собственного поглощение света в КЯ характеризуется следующими свойствами (рис. 4.1):

1) Край полосы собственного поглощения, определяемый шириной запрещенной зоны , сдвигается в область более высоких частот по сравнению с объемным полупроводником.

2) Дисперсия коэффициента поглощения в области края в общем случае носит ступенчатый характер. Каждой ступеньке соответствует дополнительный вклад в межзонное поглощение от переходов между одной из подзон валентной зоны и подзоной зоны проводимости. В связи с этим коэффициент собственного поглощения света КЯ на пороговой частоте не равен нулю, в отличие от объемного полупроводника.

3) Спектр коэффициента поглощения не зависит от поляризации света и слабо зависит от температуры.

4) В КЯ, симметричных относительно центра, поглощение света между подзонами определяется дополнительными правилами отбора, зависящими от четности состояний в подзонах.

 

Для периодических СР из КЯ волновые функции начального и конечного состояний электронов при межзонном поглощении с учетом (2.27) имеют следующий вид:

,

(4.23)

.

(4.24)

Собственные значения энергии этих функций, отсчитанные от дна зоны проводимости и потолка валентной зоны, с учетом (2.29) равны

,

(4.25)

.

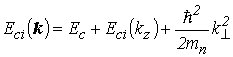(4.26)

В приближении квазидвумерного электронного газа для контравариантных СР из слабо взаимодействующих КЯ; с учетом формул (4.24) – (4.26), выражение для коэффициента поглощения имеет вид (4.21), что и для изолированной КЯ:

,

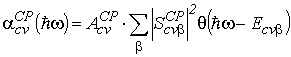(4.27)

где

;                    .

(4.28)

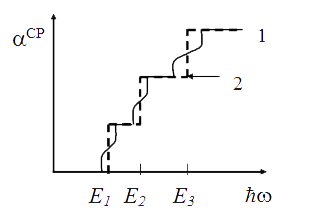
Для рассматриваемых СР свойства собственного поглощения в области края, как и следовало ожидать, совпадают со свойствами этого поглощения в отдельной КЯ (рис. 4.2). Наличие коэффициента поглощения, отличного от нуля на пороговой частоте, дает возможность использовать СР вместо объемных полупроводников для создания квантовых генераторов с существенно более низким значением порогового тока. Влияние дисперсии энергии минизон по компоненте волнового вектора , описываемой формулой (2.34), приводит к тому, что ступенчатый характер края межзонного поглощения света сглаживается (рис.4.2).

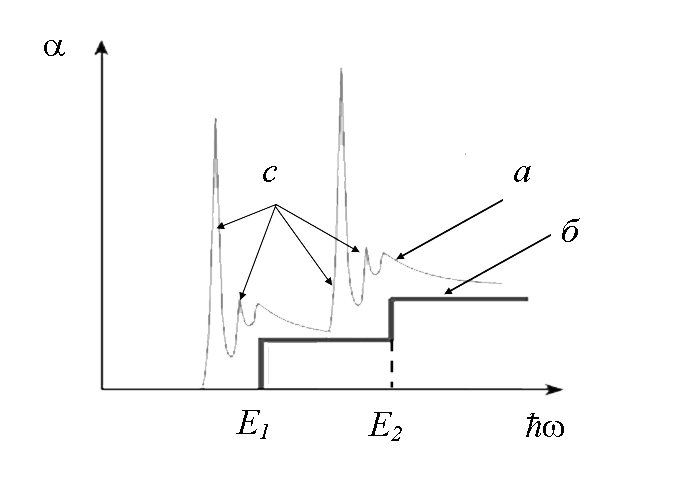
При низких температурах за счет влияния экситонных эффектов форма края собственного поглощения в изолированных КЯ и СР из слабо взаимодействующих КЯ изменяется. На рис. 4.3 приведена качественная зависимость коэффициента поглощения в области края собственного поглощения с учетом пиков поглощения на связанных экситонах и кулоновского взаимодействия электронов и дырок [1].