С учетом (2.8) формула для функции в изолированной КЯ принимает вид

,

(3.4)

где – число разрешенных состояний в подзоне номера m с энергией от до E:

.

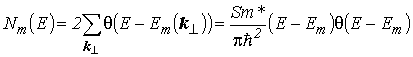(3.5)

Формула получена с помощью перехода от суммирования по к интегрированию. Фактор 2 перед суммой учитывает наличие у электрона спина. С учетом (3.2) для плотности состояний, рассчитанной на единицу площади слоя КЯ, получаем

,

(3.6)

где

(3.7)

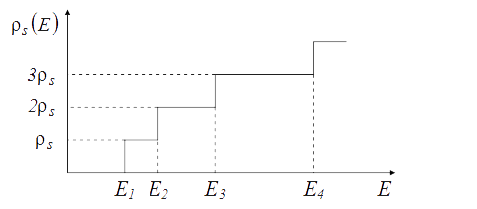
– поверхностная (двумерная) плотность состояний в двумерной подзоне КЯ, не зависящая от энергии и номера подзоны. На рис. 3.1 представлена ступенчатая зависимость двумерной плотности состояний от энергии, определяемая формулой (3.6). Характерной особенностью этой зависимости является одинаковая высота ступенек, имеющая место в приближении независимости m* от номера подзоны.

С учетом формул (3.1) и (3.6) для поверхностной концентрации носителей заряда имеем

,

(3.8)

где

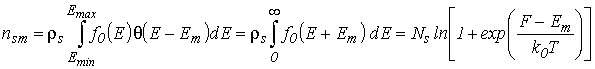(3.9)

– поверхностная концентрация в подзоне с номером m; –эффективная плотность состояний в подзоне. В одноподзонном приближении, когда носители заряда в основном находятся в нижней подзоне ()

,

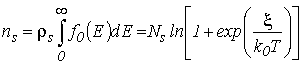(3.10)

где – приведенный уровень Ферми. Для предельных случаев невырожденного газа носителей заряда  и вырожденного из формулы (3.10) для поверхностной концентрации в одноподзонном приближении получаем

.

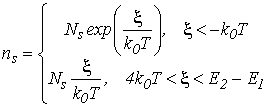(3.11)

Формула (3.11) аналогична формуле для концентрации невырожденных электронов в трехмерных структурах, если в ней заменить трехмерную объемную плотность состояний на двумерную поверхностную.

Для квантовых нитей формула (3.5) с учетом (2.20) принимает следующий вид

,

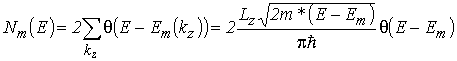(3.12)

где –длина КН. Для плотности состояний, рассчитанной на единицу длины КН – линейной плотности состояний – из формулы (3.2) с учетом (3.3) и (3.12) получаем

.

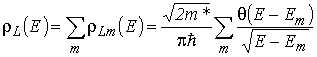(3.13)

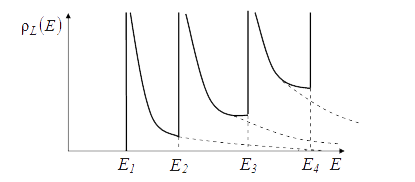
На рис. 3.2 представлена качественная зависимость функции для изолированной КН. Из рисунка следует, что эта плотность состояний является аналогом плотности состояний трехмерных структур в однородном магнитном поле. Отличием от трехмерного случая является отсутствие периодической зависимости в чередовании пиков, наличие которой в объемных полупроводниках определяется эквидистантным характером уровней Ландау.

Для линейной концентрации носителей заряда с учетом (3.1) и (3.13) после несложных преобразований получаем

.

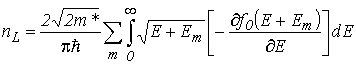(3.14)

В одноподзонном приближении для предельных случаев вырождения из формулы (3.14) следует

.

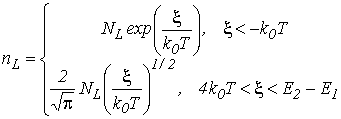(3.15)

где 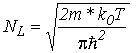– линейная эффективная плотность состояний в подзоне КН.