Для одномерной изолированной квантовой ямы с осью z, перпендикулярной ее слоям, уравнение (2.1) принимает вид

.

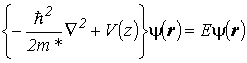(2.2)

Это уравнение допускает решение методом разделения переменных с функцией

,

(2.3)

где S – площадь сечения КЯ, перпендикулярного оси z; –двумерный волновой вектор, описывающий свободное движение вдоль КЯ. Огибающая функция с граничными условиями является решением одномерного уравнения Шредингера для движения поперек КЯ

.

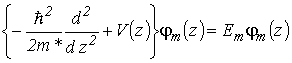(2.4)

В случае прямоугольной бесконечно глубокой КЯ шириной а, где

,

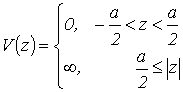решением уравнения (2.4) с граничными условиями 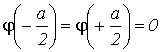является стоячая волна:

,

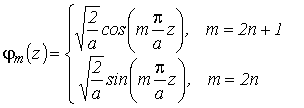(2.5)

где n – целые числа.

Как известно, для ее образования необходимо, чтобы на длине распространения укладывалось целое число полуволн:

.

(2.6)

Из этого условия следует, что волновой вектор вдоль оси z может принимать только дискретные значения

.

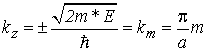(2.7)

С учетом формулы (2.7) и свободного движения вдоль КЯ полная энергия, соответствующая огибающей функции (2.3), равна

.

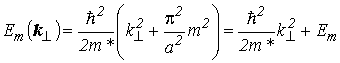(2.8)

Из формулы (2.8) для разрешенных значений энергии, соответствующих движению поперек КЯ, получаем

.

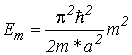(2.9)

Формула (2.9) описывает дискретный спектр размерного квантования в прямоугольной бесконечно глубокой КЯ. Разрешенные значения энергии при заданных значениях m и всех значениях представляют собой подзоны, на которые в результате размерного квантования расщепляется зона носителей заряда в отсутствие внешнего поля. Квантовое число m представляет номер подзоны.

В случае прямоугольной потенциальной ямы конечной глубины дискретные уровни энергии E_m, лежащие внутри КЯ, т.е. ниже высоты потенциального барьера , являются решениями трансцендентного уравнения

,

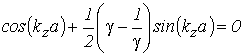(2.10)

где

;     ;

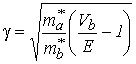(2.11)

, – эффективные массы носителей заряда полупроводников, из которого состоят потенциальная яма и барьер. Число этих уровней удовлетворяет условию

.

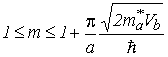(2.12)

У огибающих волновых функций появляются экспоненциальные хвосты, характерная глубина проникновения которых в потенциальные барьеры равна обратной величине коэффициента затухания

.

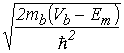В случае треугольной КЯ, характерной для МДП-структур и одиночных гетеропереходов, потенциальная энергия, ограничивающая движения вдоль оси симметрии структуры, равна

,

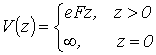(2.13)

где F – напряженность однородного электростатического поля в инверсионном слое, e – элементарный заряд. Для такой потенциальной ямы разрешенные уровни энергии приближенно можно рассчитать по формуле

.

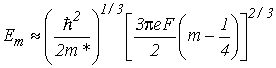(2.14)

Для параболической КЯ в легированных симметричных периодических структурах потенциальную энергию носителей заряда можно представить в виде

,

(2.15)

где

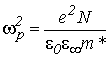(2.16)

квадрат плазменной частоты свободных носителей заряда; –концентрация ионизированной примеси в слоях n- и p-типа; –электрическая постоянная; – высокочастотная диэлектрическая проницаемость. В такой яме разрешенные уровни энергии спектра размерного квантования совпадают со спектром квантового гармонического осциллятора

.

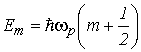(2.17)