Для квантовых нитей, в которых для определенности движение вдоль оси z будем считать свободным, потенциальная энергия является функцией координат x и y. Решением уравнения (2.1) в этом случае является огибающая функция

(2.18)

где – компонента волнового вектора, соответствующая свободному движению вдоль оси z; L – длина квантовой нити; – огибающая функция, описывающая движение в плоскости сечения, перпендикулярного оси нити, и являющаяся решением уравнения

(2.19)

с граничными условиями на бесконечности. Энергетический спектр носителей заряда в квантовой нити, соответствующий огибающим функциям (2.18), как и в случае квантовой ямы, состоит из двух частей–энергии свободного движения, являющейся непрерывной функцией , и дискретных уровней энергии размерного квантования:

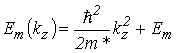(2.20)

Все уровни энергии при заданных квантовых числах m, как и в случае КЯ, образуют подзону.

В квантовой нити значку m соответствует два квантовых числа, задающих локализованное состояние двумерного движения в плоскости x,y.

В простейшем случае, когда потенциальную энергию можно представить в виде двух прямоугольных бесконечно глубоких КЯ шириной a вдоль оси x и b вдоль оси y:

(2.21)

решением уравнения (2.19) являются огибающие функции, представляющие собой произведение функций вида (2.5):

(2.22)

Энергия уровней размерного квантования, соответствующая этим функциям, равна

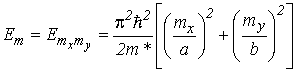(2.23)