Согласно квантовой механике выражение для коэффициента поглощения света за счет прямых оптических переходов в электронном газе полупроводниковых структур можно представить в виде [16]:

,

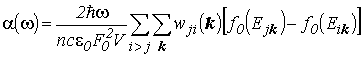(4.4)

где

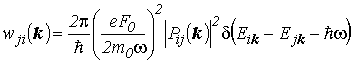(4.5)

– вероятность оптического перехода электрона из состояния с волновой функцией в состояние ; i, j – дискретные квантовые числа конечного и начального состояний (номер зоны); k – квазидискретный волновой вектор, размерность которого определяется числом степеней свободного движения электронов. В объемных полупроводниках этот вектор трехмерный, в КЯ–двумерный, в КН – одномерный, в КТ – нульмерный; , – энергии начального и конечного состояний электрона;

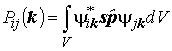(4.6)

– матричный элемент проекции оператора импульса на световой вектор; s – единичный вектор, параллельный световому вектору; –коэффициент преломления света; с – скорость света; – амплитуда светового вектора; – масса свободного электрона; – равновесная функция Ферми–Дирака, значение которой для электронов в валентной зоне можно рассматривать близким к единице, а для электронов в зоне проводимости – близким к нулю; V – объем, занимаемый электронным газом.

В области края собственного поглощения для разрешенных оптических переходов [16] в окрестности точки k=0 зависимость коэффициента поглощения от частоты с учетом (4.4) можно представить в виде

,

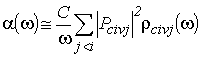(4.7)

где индекс c соответствует зоне проводимости, v – валентной зоне; С – константа пропорциональности, в области края слабо зависящая от частоты за счет показателя преломления; матричный элемент импульса ;

(4.8)

– функция оптической плотности состояний. По физическому смыслу значение этой функции равняется числу разрешенных согласно законам сохранения энергии и импульса оптических переходов электронов между подзонами vj и ci за счет поглощения фотонов с энергией от до , рассчитанному на единичный интервал энергии. Учитывая квазинепрерывный характер волнового вектора электрона, функцию оптической плотности можно рассматривать как производную по энергии перехода от числа всех возможных вертикальных переходов электронов из подзоны vj в подзону ci с энергией до :

.

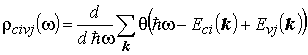(4.9)

Из формулы (4.9) следует, что функция оптической плотности является аналогом функции плотности состояний (см. (3.2)-(3.3)).