В сверхрешетках из квантовых ям носители заряда с энергией ниже потенциального барьера могут туннельным способом переходить из одной потенциальной ямы в другую. В случае периодических СР волновые функции в приближении эффективной массы являются решением уравнения (2.2) с периодической функцией потенциальной энергии вдоль оси роста (симметрии) решетки. Если ось z совпадает с осью симметрии, огибающая волновой функции согласно теореме Блоха принимает следующий вид:

.

(2.27)

– периодическая часть функции Блоха, соответствующей движению вдоль оси z:

,

(2.28)

где – период СР, состоящий из квантовой ямы и барьера шириной a и b соответственно; n – целое число. Собственные значения энергии, отвечающие функции (2.27), равны

,

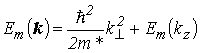(2.29)

где – периодическая функция компоненты волнового вектора , соответствующая функции :

.

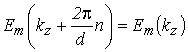(2.30)

Согласно теореме Блоха неэквивалентные значения меняются в пределах первой зоны Бриллюэна СР

,

(2.31)

принимая в ней с учетом циклического условия Борна–Кармана квазидискретные значения:

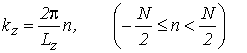
где – длина СР; N – число периодов СР.

Все уровни энергии при заданном значении m составляют минизону, в которой энергия является квазинепрерывной функцией волнового вектора k. Квантовое число m соответствует номеру минизоны.

В случае прямоугольных квантовых ям и барьеров – приближение Кронига–Пенни – значения энергии являются решением трансцендентного уравнения

 

 

,

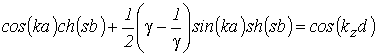(2.32)

где

;                       ; .

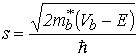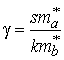(2.33)

 

В уравнении (2.32) использованы те же обозначения, что и в уравнении (2.10). При , что имеет место при и , уравнение (2.32) переходит в уравнение (2.10) для изолированных прямоугольных КЯ конечной глубины. При , когда вероятность туннелирования между КЯ становится малой, СР называются решетками со слабо взаимодействующими КЯ. Приближение, которое используется для расчета энергетического спектра и волновых функций таких СР, называется приближением сильной связи. Название этого приближения учитывает тот факт, что носители заряда за счет сильного взаимодействия с КЯ, в которой находятся, почти все время проводят в ней, лишь изредка туннелируя в другие ямы. Для энергетического спектра носителей заряда из решения уравнения (2.32) в приближении сильного взаимодействия получаем

,

(2.34)

где – решения уравнения (2.10); – ширина минизоны. На рис. 2.1 представлен энергетический спектр первой (основной) и второй (первой возбужденной) минизон, определяемый формулой (2.34).

Для основной минизоны дисперсия энергии по k_z имеет вид

.

(2.35)

При малых значениях k_z, раскладывая в ряд функцию косинуса, для носителей заряда можно ввести эффективную массу вдоль оси z:

,

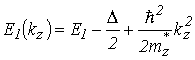(2.36)

где

.

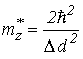(2.37)

Следовательно, энергетический спектр носителей заряда в окрестности дна минизоны с учетом энергии свободного движения вдоль КЯ можно описать с помощью тензора анизотропной эффективной массы. Значение за счет ее зависимости от ширины минизоны можно изменять в широких пределах, изменяя конструктивные параметры СР. Для узких минизон .