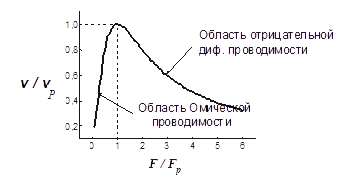При вертикальном токопереносе в области сильных классических полей вольт-амперная характеристика СР обнаруживает наличие отрицательной дифференциальной проводимости (ОДП). Наличие этого эффекта связано с периодической зависимостью энергии минизоны от квазиимпульса электрона, который существенно изменяется под действием электрического поля при наличии слабого рассеяния. Для качественного рассмотрения этого явления воспользуемся уравнениями квазиклассики. Проведем расчет плотности электрического тока вдоль оси симметрии СР – оси z, учитывая изменение квазиимпульса под действием электрического поля и сил трения согласно классическому уравнению движения

,

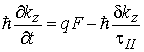(5.31)

где           – отклонение компоненты волнового вектора от равновесного значения; – среднее значение продольного времени релаксации, не зависящее от энергии. Решением этого уравнения для стационарного тока является

.

(5.32)

Для расчёта плотности продольного (вертикального) тока воспользуемся общей формулой

,

(5.33)

где – полная энергия движения носителя заряда, отсчитанная от дна минизоны; – энергия свободного движения вдоль КЯ; – энергия движения вдоль оси СР с учетом (2.35), равная

;

(5.34)

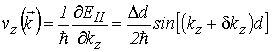(5.35)

– скорость продольного движения электрона с заданным значением в электрическом поле; – дрейфовая скорость. Равновесная функция Ферми–Дирака в приближении двумерного газа для невырожденных носителей заряда в минизоне равна

.

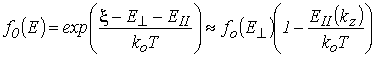(5.36)

С учётом формул (5.33), (5.35) и (5.36) для продольной дрейфовой скорости получаем

,

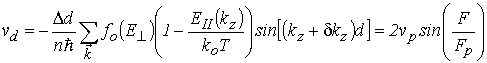(5.37)

где

;

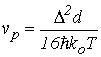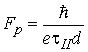(5.38)

При выводе формулы (5.37) было учтено, что концентрация электронов в приближении двумерного газа равна

.

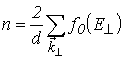(5.39)

Из формулы (5.37) вытекает, что продольная дрейфовая скорость зависит от электрического поля по гармоническому закону. Следовательно, при  c ростом напряжённости поля дрейфовая скорость и связанная с ней плотность продольного тока будут убывать, т.е. дифференциальная проводимость становится отрицательной.

Точный расчет плотности вертикального тока в сильных классических электрических полях основан на решении уравнения Больцмана (5.1) в приближении времени релаксации

,

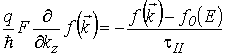(5.40)

с граничными условиями периодичности по обратным векторам СР

,

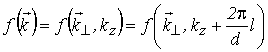(5.41)

где                l – целое число. Согласно аналитическому решению этого уравнения [19]

.

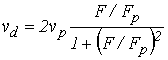(5.42)

Из этой формулы следует, что в сильных классических электрических полях, удовлетворяющих условию , дифференциальная проводимость становится отрицательной. При этом дрейфовая скорость, в отличие от элементарной теории (см. (5.37)), всегда остаётся положительной. В случае слабых классических полей  из формул (5.37) и (5.42) в согласии с законом Ома получаем линейную зависимость дрейфовой скорости от поля (см. (5.25)):

.

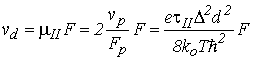(5.43)

Для вырожденного электронного газа в согласии с (5.28) формула для максимальной дрейфовой скорости принимает вид

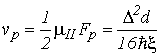(5.44)

Из сравнения формул (5.38) и (5.44) следует, что с ростом вырождения электронного газа максимальное значение продольной дрейфовой скорости уменьшается.

На рис. 5.1 представлена зависимость продольной дрейфовой скорости от напряжённости электрического поля, описываемая формулой (5.42).

 

Из анализа формулы (5.42) вытекает критерий слабого

(5.45)

и сильного

(5.46)

классических электрических полей для вертикального переноса в СР. Согласно критерию слабого поля энергия, которую должен получать носитель заряда на периоде СР в этом поле, должна быть гораздо меньше неопределенности энергии за счет рассеяния.