5.1. Неравновесная функция распределения в низкоразмерных структурах

Как известно, анализ электропроводности носителей заряда в полупроводниках в области классических электрических полей проводится с помощью неравновесной функции распределения. В случае низкоразмерных полупроводниковых структур и упругих механизмов рассеяния эта функция – в однородном электрическом поле является решением кинетического уравнения Больцмана

,

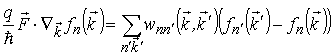(5.1)

где q – заряд электрона или дырки; – вероятность рассеяния за единицу времени из состояния в ; n и n´ – номера подзон или минизон. Наличие межподзонного или межминизонного рассеяния, которое проявляет себя при большой концентрации носителей, существенно усложняет решение уравнения (5.1). Для простоты в дальнейшем будем использовать одноминизонное приближение, считая, что все носители заряда находятся в нижней (основной) подзоне (минизоне), испытывая только внутриподзонное (внутриминизонное) рассеяние.

В области слабых электрических полей, когда отклонение функции распределения от равновесной можно считать малым, уравнение (5.1) в одноминизонном приближении принимает следующий вид:

,

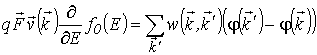(5.2)

где ; – энергия носителя заряда в основной подзоне или минизоне; – скорость носителя заряда.

С учетом анизотропного характера низкоразмерных полупроводниковых структур для решения уравнения (5.2) можно использовать приближение тензора времени релаксации. В этом приближении для решения уравнения (5.2) получаем

,

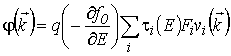(5.3)

где

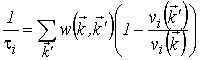(5.4)

– компонента тензора времени релаксации в главных осях тензора обратной эффективной массы. Используя известное выражение для плотности электрического тока с учетом (5.3), получаем

,

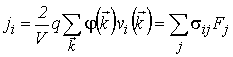(5.5)

где

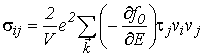(5.6)

– компонента тензора удельной проводимости.