Для двумерного газа носителей заряда в одномерных КЯ неравновесная добавка к функции распределения (5.3) с учетом симметрии запишется в виде

,

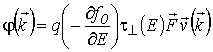(5.7)

где . При этом скалярное значение удельной проводимости принимает известное выражение

,

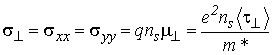(5.8)

где n_S – поверхностная концентрация (3.10); – подвижность; – эффективная масса носителей заряда двумерного газа в КЯ; – усредненное по энергии носителей заряда время релаксации, выражение для которого с учетом (2.8) и (3.7) имеет следующий вид:

.

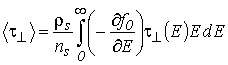(5.9)

Как известно [16], в объемных полупроводниках в приближении упругого рассеяния зависимость времени релаксации от энергии и температуры для основных механизмов рассеяния носит степенной характер

,

(5.10)

где – обозначение объемного времени релаксации с учетом трехмерного характера движения носителей заряда. Изменение энергетического спектра и плотности состояний за счет размерного квантования для двумерного газа носителей заряда приводит к следующей формуле [13]:

,

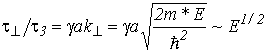(5.11)

где g – численный множитель порядка единицы; a – ширина КЯ. С учетом (5.10) и (5.11) зависимость двумерного времени релаксации от энергии и температуры принимает следующий вид:

.

(5.12)

Для невырожденного двумерного газа при заданной температуре среднее значение двумерного волнового вектора , где – среднее значение тепловой энергии носителей заряда. В одноподзонном приближении среднее значение энергии должно быть много меньше зазора между подзонами, т.е. . С учетом вышесказанного из формулы (5.11) следует, что . То есть при прочих равных условиях наличие размерного квантования приводит к уменьшению времени релаксации. Вывод остается неизменным и для вырожденного газа.

С учетом полученных выше формул проведем анализ температурной зависимости подвижности двумерного газа в КЯ. Согласно формуле (5.8) температурная зависимость подвижности двумерных носителей заряда определяется температурной зависимостью среднего времени релаксации. Для невырожденного газа носителей заряда среднее значение двумерного времени релаксации, рассчитанное по формуле (5.9) с учетом (3.7), (3.10) и (5.12), равняется

,

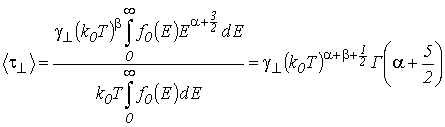(5.13)

где Г(n) – гамма-функция. В объемных полупроводниках с невырожденным трехмерным газом зависимость среднего времени релаксации от температуры определяется формулой [10]:

.

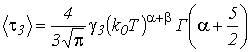(5.14)

В табл. 5.1 для основных механизмов рассеяния приведены значения коэффициентов a, b [16] и .

Таблица 5.1

Параметры основных механизмов рассеяния носителей заряда трех- и двумерного газа полупроводников

Вид рассеяния	a	b	a+b	d
Акустические фононы (АКФ)	-1/2	-1	-3/2	-1
Полярные оптические фононы (ПОФ)	+1/2	-1	-1/2	0
Ионы примеси (ИОН)	+3/2	0	+3/2	2
Нейтральные примесные атомы (НПА)	0	0	0	+1/2

Согласно данным, приведенным в таблице, наличие размерного квантования в КЯ существенно изменяет температурную зависимость времени релаксации и подвижности для отдельных механизмов рассеяния. Следует отметить, что при рассеянии на ПОФ, которое при высоких температурах в полупроводниках А³В⁵ является основным, среднее время релаксации двумерных носителей заряда не зависит от температуры. При рассеянии на ионах примеси оно растет быстрее, чем в объемных полупроводниках, а при АКФ-рассеянии убывает медленнее.

Для вырожденного газа носителей заряда, заменяя в формуле (5.9) производную от равновесной функции распределения на дельта-функцию, для среднего значения двумерного времени релаксации с учетом (3.15) получаем

.

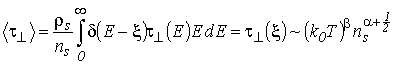(5.15)

Для вырожденного газа в объемных полупроводниках [16]

.

(5.16)

Из вышеприведенных формул следует, что, в отличие от трехмерного вырожденного газа, подвижность двумерного вырожденного газа, определяемая АКФ-рассеянием, не зависит от концентрации носителей заряда, т.е. от уровня легирования.

С учетом проведенного анализа подвижности носителей заряда в одномерных КЯ в области омической проводимости можно сделать следующие выводы. При прочих равных условиях наличие размерного квантования

1) уменьшает усредненное по энергии время релаксации, а следовательно, и подвижность;

2) в случае невырожденного газа носителей заряда изменяет по сравнению с объемной температурную зависимость подвижности для отдельных механизмов рассеяния;

3) в случае вырожденного газа носителей заряда изменяет по сравнению с объемной зависимость подвижности от концентрации носителей для отдельных механизмов рассеяния.