Влияние однородного электрического поля на энергетический спектр носителей заряда в изолированных КЯ и СР из КЯ тоже, как и в случае с магнитным полем, существенно зависит от направления вектора напряженности электрического поля F относительно слоев гетероструктур. Наиболее существенно это влияние проявляется в сверхрешетках, если направление F перпендикулярно этим слоям. В этом случае уравнение Шредингера (2.1) с периодической потенциальной энергией вдоль оси z и потенциальной энергией электрона в однородном электрическом поле принимает вид

,

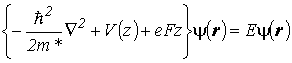(2.57)

 

где ; d – период СР. Решения этого уравнения методом разделения переменных имеют вид (2.3) с функцией , которая является решением уравнения Шредингера для одномерного движения электрона вдоль оси симметрии СР

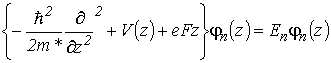(2.58)

с нулевыми граничными условиями . В случае изолированной КЯ этому уравнению соответствует дискретный спектр разрешенных уровней энергии, значение которых является функцией электрического поля. То есть характер энергетического спектра для изолированной КЯ в однородном электрическом поле не меняется.

Для СР с периодическим потенциалом , в приближении огибающих функций [10], это уравнение с нулевыми граничными условиями принимает вид

,

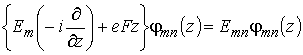(2.59)

где – зависимость энергии в минизоне СР с номером m, определяемая формулой (2.31), в которой компонента волнового вектора заменена на дифференциальный оператор. С учетом симметрии уравнения (2.59) огибающую волновой функции и ее собственные значения энергии можно представить в виде

,       ,        ()        ,

(2.60)

где – частота Ванье–Штарка; N – число периодов СР. Функция является решением уравнения (2.58) при . Таким образом, зная одно из решений уравнения (2.59) для некоторой минизоны, можно найти все остальные. Из формулы (2.60) следует, что каждая минизона в электрическом поле, перпендикулярном слоям СР, претерпевает штарковское расщепление на N дискретных эквидистантных уровней. Функции являются локализованными в окрестности КЯ с номером n. Область локализации зависит от ширины минизоны и не зависит от номера КЯ

.

(2.61)

В сильных электрических полях при условии функция становится локализованной внутри одной КЯ с номером n. Выполнение этого условия в СР соответствует штарковской локализации уровней.

С учетом вышесказанного в приближении огибающих решением уравнения (2.57) является функция

,          []

(2.62)

с собственным значением энергии

.

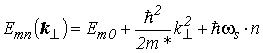(2.63)

Согласно (2.63) в случае штарковской локализации уровней в каждой КЯ сверхрешетки имеется спектр разрешенных уровней энергии, аналогичный спектру изолированной КЯ. Совокупность разрешенных уровней энергии с заданным номером минизоны называется «штарковской лесенкой». Следовательно, в квантующем электрическом поле квазинепрерывный спектр каждой минизоны СР превращается в спектр из эквидистантных дискретных уровней «штарковской лесенки».

Если вектор F направлен параллельно слоям гетероструктуры, уравнение (2.57) для изолированной КЯ принимает вид

,

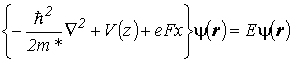(2.64)

а решение этого уравнения методом разделения переменных

,

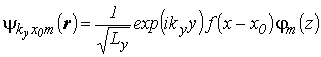(2.65)

где – решение уравнения (2.2) для уровней размерного квантования в изолированной КЯ без поля; – решение одномерного уравнения Шредингера для движения вдоль поля

,

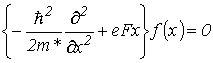(2.66)

с нулевыми граничными условиями . Полная энергия, соответствующая функции (2.65), равна

.

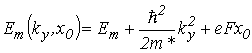(2.67)

Для СР из КЯ функцию в (2.65) нужно заменить на (2.28), а в (2.67) – на (2.30).

Из вышесказанного следует, что в продольном электрическом поле в КЯ и сверхрешетках из КЯ энергетический спектр носителей заряда изменяется таким же образом, как и в трехмерных структурах.