Ситуация  называется равновесной по Нэшу в см.-стратегиях (равновесием Нэша в см.-стратегиях), если справедливо

.

(3.6)

      Теорема Нэша для смешанных стратегий. Если равновесная по Нэшу см.-стратегия  игрока  входит в равновесие Нэша  и приписывает положительную вероятность реализации чистой стратегии , то

.

(3.7)

Данная теорема является конструктивной, так как дает рецепт поиска равновесных по Нэшу см.-стратегий.

      Пример 3.4. Рассмотрим игру «Монетки» с платежной биматрицей

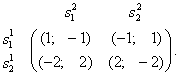
      Пусть   и   – произвольные см.-стратегии игроков  и  соответственно. Предположим, что  в  равновесной по Нэшу ситуации  вероятность реализации любой из имеющихся стратегий игроков отлична от нуля, т.е. , . Тогда в соответствии с (3.7) получаем следующую систему:

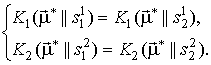(3.8)

      Подстановка заданных значений элементов платежной биматрицы в (3.2) дает, согласно (3.8) систему уравнений

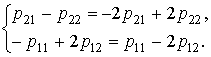(3.9)

      Добавление к (3.9) условий нормировки

дает систему линейных уравнений:

имеющую единственное решение

.

      В итоге равновесными по Нэшу см.-стратегиями являются следующие:

 и .

Отметим, что равновесные по Нэшу см.-стратегии совпали с полученными  в примере 3.3 защитными см.-стратегиями.