Введение понятия смешанной стратегии является расширением множества стратегий игроков, поскольку любая чистая стратегия может быть рассмотрена как частный случай смешанной. Действительно,

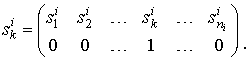
Если каждый из игроков применяет смешанную стратегию , то тем самым они создают ситуацию в смешанных стратегиях

,

которая определяет случайный механизм реализации набора чистых стратегий игроков. В этом случае любая ситуация  возникает случайным образом. Игроки действуют независимо, поэтому вероятность  возникновения конкретной ситуации  равна произведению вероятностей реализации конкретных чистых стратегий :

.

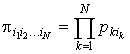(3.1)

При этом должно выполняться условие нормировки .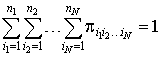

В качестве значения выигрыша i-го игрока в ситуации смешанных стратегий  принимается математическое ожидание его случайного выигрыша в ситуации, реализованной случайным образом с вероятностью , определенной в (3.1):

.

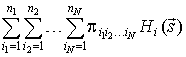(3.2)

Здесь  функция выигрыша игрока  в ситуации .

Введем обозначение

.

(3.3)

Пусть  – произвольная смешанная стратегия игрока  в игре . Умножив (3.3) на  и просуммировав по всем , получаем .

Теперь дадим строгое определение игры, получаемой из игры  с применением смешанных стратегий.

Игра , в которой множество N игроков,  – множество смешанных стратегий каждого игрока , а функция выигрыша в ситуации смешанных стратегий  определяется равенством (3.2) (ссылка на кадр 67), называется смешанным расширением игры .