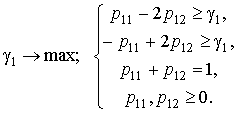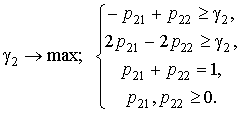Пример 3.3. Совершенно аналогично в условиях игры «Монетки» согласно (3.4) защитные см.-стратегии  и  могут быть найдены из решения следующих задач:

Задача игрока :		Задача игрока :

Решая данные задачи линейного программирования графически или симплекс-методом, получаем следующие оптимальные защитные см.-стратегии:  и . При этом игроки получат средний гарантированный выигрыш в размере .

Если трактовать вероятности выбора чистых стратегий как относительные частоты наступления событий, то полученные значения для  и  можно интерпретировать следующим образом: в случае многократного повторения игры оптимальными  стратегиями игроков являются следующие: игрок  выкладывает 1 руб. в два раза чаще, чем 2 руб.; игрок  обе монетки выкладывает с одинаковой частотой.