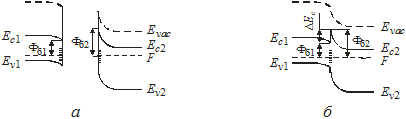По современным представлениям, у поверхности полупроводника существуют локализованные электронные состояния, проникающие в полупроводник на глубину порядка десятых долей нм. Причиной появления таких локализованных состояний является резкое нарушение периодичности расположения атомов в результате обрыва кристаллической решетки.

Перераспределение носителей заряда между этими поверхностными состояниями и прилегающим объемом полупроводника приводит к образованию в полупроводнике области пространственного заряда, приповерхностному изгибу энергетических зон и «закреплению» уровня Ферми на поверхности [4,5]. В полупроводниках с преимущественно ковалентным типом химической связи (к которым относятся и полупроводниковые соединения типа A^IIIB^V) поверхностный уровень Ферми закрепляется в определенной части запрещенной зоны – вблизи так называемого уровня локальной электронейтральности в полупроводнике [8,9].

Уровень локальной электронейтральности E_LNL является характеристикой данного полупроводника, и его положение определяется параметрами объемного энергетического спектра полупроводника. Рассчитанное для ряда полупроводников положение уровня E_LNL относительно дна зоны проводимости [9] представлено в Приложении 2.

При нанесении слоя металла на свободную поверхность полупроводника и образовании барьера Шоттки величина имевшегося изгиба энергетических зон почти не изменяется. Для подтверждения этого в Приложении 2 приведены также типичные значения высоты барьера Шоттки Φ_б, измеренные в контактах Au и Al c полупроводниками n-типа.

При образовании резкого гетероперехода вблизи гетерограницы, где нарушается периодичность потенциала кристаллической решетки, возникают локальные электронные состояния (аналогичные рассмотренным выше поверхностным состояниям) с уровнями в запрещенной зоне одного или обоих полупроводников. При этом положение уровня Ферми вблизи гетерограницы оказывается близким к положениям уровней локальной электронейтральности каждого из контактирующих полупроводников.

В соответствии с данными представлениями гетеропереход можно рассматривать как соединение двух полупроводников (или барьеров Шоттки), у которых уже сформированы области пространственного заряда и существуют приповерхностные изгибы зон еще до контакта (рис. 5.3, а, б) [4].

Рис. 5.3. Построение энергетической диаграммы анизотипного p–N-гетероперехода при наличии локальных состояний у границ полупроводников [4]

 

В этом случае величину скачка дна зоны проводимости в гетеропереходе можно оценить как разность расчетных уровней локальной электронейтральности в исходных полупроводниках:

$\Delta E_c={\text{(}{E}_c-E_{LNL}\text{)}}_2-{\text{(}{E}_c-E_{LNL}\text{)}}_1$

(5.6)

или как разность экспериментальных высот барьеров Шоттки для электронов в них:

$\Delta E_c={\Phi }_{\text{б}2}-{\Phi }_{\text{б}1}$.

(5.7)

Величина DE_v при этом по-прежнему выражается формулой (5.3).