Лемма 2. Пусть s=s0s1… - произвольная л.р.п. n-го порядка над полем F. Тогда для любого целого t ≥ 0 существуют a0, a1, …, an–1 в F, что для всех i ≥ 0 справедливо:
si+t =  . . |
(3) |
Доказательство. Если t < n, то требуемые равенства верны при at = 1 и aj = 0 для j ≠ t. При t ≥ n они доказываются индукцией по t, ибо при t = n они верны в силу (2) и по предположению индукции можно записать:
si+t+1 = si+1+t = 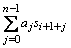 , i ≥ 0. , i ≥ 0. |
(4) |
Для каждого j = 0, 1, …, n-1 выполняется j+1 ≤ n, поэтому по предположению индукции для любого такого j существуют b0, b1, …, bn–1 в F, что для всех i ≥ 0
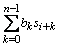 .
.После замены в (4) каждого si+1+j равным ему выражением последнего вида, получим требуемые равенства для si+t+1. 
Пусть далее s = s0s1… есть m-последовательность n-го порядка над полем F = Zp, т.е. q = p и членами в s являются числа 0, 1, …, p-1.
Лемма 3. Пусть a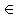 F, a ≠ 0 и t ≥ 0. Тогда для высказываний:
F, a ≠ 0 и t ≥ 0. Тогда для высказываний:
(i) si+t = asi для всех i ≥ 0;
(ii) t = 0 mod (1 + p + p2 + … + pn–1)
справедливы следующие утверждения: (i)  (ii) и
(ii) и 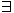 t ≤ pn−2[(i) & (ii)].
t ≤ pn−2[(i) & (ii)].
Доказательство. Пусть верно (i). Тогда ввиду теоремы Ферма si+(p–1)t = ap–1si = si для всех i ≥ 0, что возможно только при условии, что (p-1)t кратно периоду последовательности s, т.е. (p-1)t = k(pn -1) для некоторого целого k, откуда t = k(pn -1)/(p-1) = k(1 + p + p2 + … + pn–1), т.е. верно (ii).
Для доказательства второго утверждения вычислим вектор (as0) (as1) … (asn–1). По лемме 1 это будет вектор stst+1…st+n–1 для некоторого t ≤ pn−2, т.е. st = as0, st+1= as1, …, st+n–1= asn–1. Применяя далее индукцию по i, предположим, что si+t = asi+0, si+t+1 = asi+1, …, si+t+n–1 = asi+n–1 для некоторого i ≥ 0, и, пользуясь (2), запишем:
 = −
= −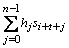 = si+n+t.
= si+n+t.Этим доказано (i). Из него по предыдущему следует (ii). 