Пусть F – конечное поле, |F| = q и n – натуральное число. Линейной рекуррентной последовательностью (кратко: л.р.п.) n-го порядка над полем F называется всякая последовательность s = s0s1… элементов поля F, являющаяся решением следующей системы рекуррентных уравнений:
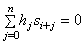 , i = 0, 1, …, , i = 0, 1, …, |
(1) |
где h0, h1, …, hn – некоторые фиксированные элементы поля F, h0 ≠ 0 и hn = 1. Многочлен h(x) = h0 + h1x + … + hn-1xn-1 + xn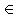 F[x] называется характеристическим многочленом данной л.р.п. Система уравнений (1), записанная в виде:
F[x] называется характеристическим многочленом данной л.р.п. Система уравнений (1), записанная в виде:
si+n = − 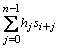 , i = 0, 1, …, , i = 0, 1, …, |
(2) |
указывает правило, по которому при любых заданных в F значениях s0, s1, …, sn–1, представляющих собой начальное условие системы, вычисляется в s сначала значение sn, затем по известным s1, …, sn – значение sn+1 и т.д., по sisi+1…si+n–1 – значение si+n.
Разным начальным условиям рассматриваемой системы уравнений отвечают разные ее решения, поэтому количество всех решений системы равно qn. При s0s1…sn–1 = 00…0 все символы в s равны 0, и такая л.р.п. называется нулевой. Поскольку уравнения в системе линейны, то любая линейная комбинация их решений будет снова решением, а все решения образуют векторное пространство над F. Его базис состоит из решений, отвечающих единичным векторам начальных условий 10…0, 01…0, …, 00…1. Таким образом, множество всех л.р.п. n-го порядка с одним и тем же характеристическим многочленом является векторным пространством размерности n над полем F.
Последовательность s = s0s1s2… называется периодической, если существует натуральное m такое, что si = si+m для всех i ≥ 0. Наименьшее m с этим свойством называется периодом последовательности s.