В последовательности s = s0s1s2… подпоследовательность z = sisi+1…si+r–1, где i ≥ 0 и r > 0, называется отрезком длины r. При i = 0 отрезок z является префиксом последовательности s. Если si = si+1 = … = si+r–1 = a ≠ si+r и, кроме того, при i > 0 верно si–1 ≠ a, а при i = 0 верно sqn–1 ≠ a, то отрезок z называется серией элемента a, или, коротко, a-серией. Для двух последовательностей u и v говорят, что v входит в u, если v является отрезком в u.
Пусть далее s = s0s1… есть m-последовательность n-го порядка над полем F из q элементов, s′ = s0s1…sqn–2 – ее префикс длины qn–1 и 1 ≤ r. Назовем s′ циклом последовательности s. Будем говорить, что вектор из F r встречается в s′, если он входит в s в качестве отрезка, начинающегося в s′. Положим S = {sisi+1…si+n-1: i = 0, 1, …, qn–2}. Это есть множество всех векторов в F n, встречающихся в цикле s′ и, значит, во всей последовательности s. Пусть также 0r есть последовательность из r символов 0 – нулевой вектор в F r.
Лемма 1. S = F n–{0n}, т.е. каждый ненулевой вектор из F n встречается в s′ ровно один раз, а нулевой вектор длины n в s′ не встречается.
Доказательство. |S| = qn–1, так как иначе период s будет меньше qn–1; кроме того, 0n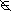 
S, так как иначе s = 00… . 
Теорема 2. В цикле s′ каждый ненулевой вектор из F r встречается qn–r раз, а нулевой – qn–r–1 раз.
Доказательство. В любой последовательности длины n имеется ровно (n–r+1) отрезков длины r ≤ n, поэтому во все векторы в F n каждый вектор из F r входит (как отрезок) одно и то же число раз, и это число равно (n–r+1)qn/qr = (n–r+1)qn–r. Ввиду леммы 1 в векторы множества S столько же раз входит каждый ненулевой вектор F r, а нулевой – на n–r+1 раз меньше, т.е. (n–r+1)(qn–r–1) раз. По определению S каждый отрезок длины r, встречающийся в s′, входит в n–r+1 векторов в S. Следовательно, в s′ каждый ненулевой вектор из F r встречается (n–r+1)qn–r/(n–r+1) = qn-r раз, а нулевой – (n–r+1)(qn–r–1)/(n–r+1) = qn–r –1 раз.
Следствие. В цикле s′ каждый ненулевой элемент поля F встречается qn–1 раз, а нуль – qn–1–1 раз.