Если условия (5.46) для сильных электрических полей не выполняются, что имеет место при наличии узких минизон или интенсивного рассеяния, то вертикальный перенос носителей заряда в СР приобретает квантовый характер. Для его описания необходимо учитывать изменение энергетического спектра и волновых функций электронов под действием поля, а также переход от классического статистического описания с помощью функции распределения к квантовому, в основе которого лежит расчет матрицы плотности [17]. Ввиду математической сложности, связанной с учетом указанных особенностей, анализ вертикальной квантовой проводимости проведем, используя качественные квазиклассические соображения.

Продольное протекание тока в квантовом электрическом поле происходит за счет туннелирования носителей заряда через потенциальные барьеры СР с последующей передачей избытка энергии либо в виде излучения фотонов, либо, что наиболее вероятно, колебаниям решетки, т.е. излучения фононов. При этом в процессе туннелирования может измениться как номер «штарковской лестницы» – минизоны (см. (2.62)), так и поперечный квазиимпульс. Последнее возможно только при наличии рассеяния. В условиях штарковской локализации () уровней минизоны в пределах периода СР туннелирование электронов возможно только между соседними КЯ.

Рассмотрим туннелирование электрона из первой минизоны и КЯ с номером 0 в соседнюю КЯ с номером 1 (направление поля совпадает с направлением  оси z). В случае упругого рассеяния при туннелировании через барьер согласно закону сохранения энергии должно выполняться условие для поперечного волнового вектора, которое с учётом (2.63) можно представить в виде

,

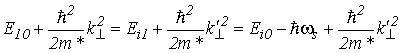(5.47)

где и – волновые векторы начального и конечного состояний электрона. Для изменения кинетической энергии поперечного движения из (5.47) имеем

.

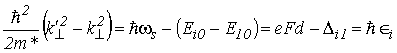(5.48)

Если расстройка , то данное туннелирование называется нерезонансным и наоборот. Из (5.48) следует, что нерезонансное туннелирование, в отличие от резонансного, должно обязательно сопровождаться рассеянием, связанным с изменением поперечного волнового вектора. Следовательно, вероятность нерезонансного туннелирования и плотность тока, связанная с ним, должны быть намного меньше, чем для резонансного. Причем с ростом по абсолютной величине вероятность нерезонансного туннелирования и плотность соответствующего тока должны убывать, так как при этом увеличивается изменение волнового вектора.

С учетом сказанного плотность вертикального электрического тока в одноминизонном приближении () можно представить в виде

,

(5.49)

где           – парциальная плотность электрического тока, связанная с туннелированием электронов из «штарковской лесенки» первой минизоны на уровни «штарковской лесенки» i-й минизоны соседней КЯ. Без учёта разогрева электронного газа, в приближении упругого рассеяния и однородного электрического поля формула для парциальной плотности тока в окрестности , рассчитанная с помощью матрицы плотности, имеет следующий вид [13]:

,

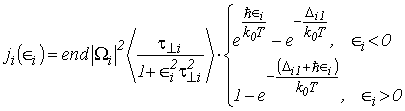(5.50)

где n – концентрация электронов; – поперечное время фазовой релаксации – величина, близкая к поперечному времени релаксации и связанная с релаксацией поперечного импульса при туннелировании;

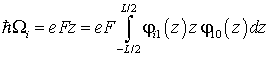(5.51)

– матричный элемент, определяющий вероятность туннельного перехода между соседними КЯ;

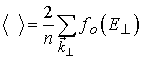(5.52)

– усреднение по поперечному волновому вектору с равновесной функцией Ферми - Дирака. Согласно (5.50) зависимость парциальной плотности тока от величины расстройки носит резонансный характер. При резонансном туннелировании парциальная плотность тока имеет максимум. С учётом (5.48) это соответствует значению напряженности поля , при этом плотность полного тока (5.49) будет определяться в основном резонансным значением парциального тока

.

(5.53)

В области слабых квантовых полей при согласно (5.50) для плотности вертикального тока получаем

.

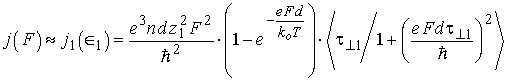(5.54)

В приближении двумерного газа () и слабого рассеяния (), что соответствует наличию штарковского расщепления, формула (5.54) для плотности вертикального тока принимает простой вид

.

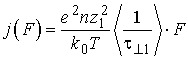(5.55)

В случае сильного рассеяния , что соответствует условию и штарковским расщеплением можно пренебречь, вертикальный перенос изначально является квантовым и описывается формулой

.

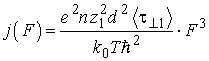(5.56)

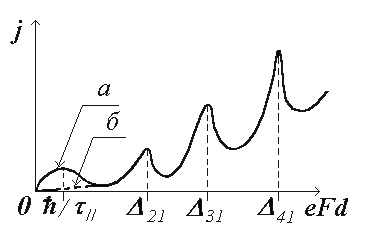
Таким образом, при условии штарковской локализации плотность тока будет пропорциональна F, если выполняется условие слабого рассеяния, и пропорциональна F³ в случае сильного рассеяния. Очевидно, при очень слабом взаимодействии КЯ, когда , ВАХ в области слабых полей будет описываться формулой (5.56) и область омической проводимости практически будет отсутствовать [13]. На рис. 5.2 представлен общий вид ВАХ нелегированной СР: а) в случае слабого рассеяния с наличием ОДП и б) сильного рассеяния с отсутствием ОДП в области классических полей.

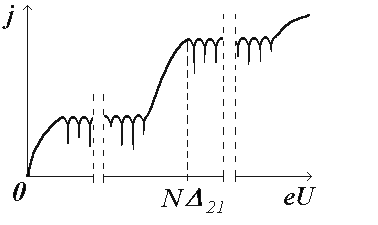
Как показал эксперимент, вольт-амперная характеристика, представленная на рис. 5.2, имеет место в собственных или слабо легированных СР. Если легирование КЯ приводит к достаточной высокой концентрации носителей, то характер ВАХ существенно изменяется. При этом ВАХ распадается на участки, в которых плотность тока монотонно растет, и участки, в которых наблюдаются многочисленные осцилляции. Природа последних связана с появлением у анода домена сильного поля, причиной которого является неустойчивость распределения плотности электронного газа вдоль оси СР при ОДП (рис. 5.3). С ростом приложенного к СР напряжения U размеры этого домена увеличиваются. Как показал анализ [20], число осцилляций в отдельной области равняется числу периодов сверхрешетки. Из этого следует, что каждая осцилляция на ВАХ соответствует увеличению размера домена сильного поля на период СР. При значениях напряжения, соответствующего на ВАХ области осцилляций, СР имеет область слабого поля у катода и сильного – у анода. Эти поля являются практически однородными, а переходная область между ними имеет размеры порядка одного периода СР.

Согласно уравнению непрерывности плотность электрического тока, протекающего через домены сильного и слабого полей, должна быть одинакова, а проводимость σ_w в области слабого поля должна быть больше, чем проводимость σ_h в области сильного поля. Следовательно, проводимость σ_w должна определяться резонансным переносом, а σ_h – нерезонансным туннелированием. Когда домен сильного поля охватит всю СР, увеличение смещения приводет к монотонному росту плотности тока, связанному с переходом в однородном электрическом поле от нерезонансного туннелирования к резонансному на всех периодах СР. С дальнейшим ростом смещения у анода снова появляется домен сильного поля, в котором происходит нерезонансное туннелирование электронов со «штарковских» уровней первой минизоны на «штарковские» уровни выше лежащей минизоны соседней КЯ (рис. 5.3). При этом в области слабого поля перенос остается резонансным. Если вышележащей минизоны в КЯ нет, то туннелирование идет в область «почти» непрерывного спектра энергий над потенциальными барьерами. Таким образом, каждая область осцилляций на ВАХ соответствует резонансному переносу в области домена слабого поля и нерезонансному переносу в домене сильного поля. Как показали дальнейшие исследования [21], домены сильного поля могут возникать не только у анода и дрейфовать вдоль поля, вызывая колебания тока по аналогии с эффектом Ганна.