Влияние магнитного поля на энергетический спектр и волновые функции носителей заряда в квантовых ямах определяется с помощью уравнения Шредингера. Без учета энергии взаимодействия собственного магнитного момента с магнитным полем это уравнение получается из уравнения (2.1), в котором оператор импульса следует заменить на оператор обобщенного импульса

,

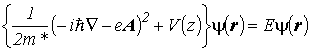(2.49)

 

где A – векторный потенциал индукции магнитного поля []. Решение этого уравнения существенно зависит от направления вектора B относительно плоскости двумерного слоя. Рассмотрим два случая. В первом случае этот вектор будет направлен вдоль плоскости двумерного слоя – предположим, по оси x. Во втором случае – перпендикулярно этому слою.

В первом случае векторный потенциал для однородного магнитного поля можно выбрать в виде . При этом уравнение (2.49) для бесконечно глубокой прямоугольной КЯ принимает вид, допускающий решение методом разделения переменных с функцией

.

(2.50)

Эта функция описывает состояния свободного движения электрона вдоль оси x и локализованного движения в плоскости yz. Локализованному движению соответствует функция , которая является решением уравнения

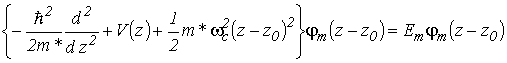
с нулевыми граничными условиями , где 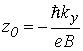; – циклотронная частота. Это уравнение является аналогом уравнения квантового гармонического осциллятора, совершающего колебания относительно точки равновесия z₀, движение которого дополнительно ограничено квантовой ямой. Собственные значения энергии E_m, соответствующие этому уравнению, представляют собой дискретные уровни.

Влияние магнитного поля на энергетический спектр, очевидно, будет возрастать, если ширина КЯ будет увеличиваться. При условии

,

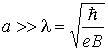(2.51)

где λ – магнитная длина, равная по величине радиусу характерной орбиты носителя заряда в магнитном поле, собственные значения энергии будут равны энергиям гармонического квантового осциллятора

.                ().

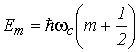(2.52)

Для полупроводников в магнитном поле эти энергии носят название уровней Ландау.

При ограничение в движении, связанное с магнитным полем, будет незначительным и для бесконечно глубокой прямоугольной КЯ формула (2.52) перейдет в формулу (2.9). Из формул (2.9) и (2.52) следует, что при условии (2.51) зазор между уровнями размерного квантования с ростом магнитного поля возрастает. Таким образом, с помощью продольного магнитного поля можно влиять на энергетический спектр в КЯ.

Собственные значения энергии в приближении огибающих волновых функций вида (2.50) являются вырожденными по квантовому числу k_y и имеют вид (2.20), где k_z нужно заменить на k_x. Из этого следует, что КЯ в продольном магнитном поле является аналогом квантовой нити.

Во втором случае для магнитного поля, поперечного двумерному слою и направленного вдоль оси z, векторный потенциал можно выбрать в виде . В этом случае решением уравнения (2.49) вместо функции (2.50) будет функция

,

(2.53)

где – огибающая волновой функции для уровней размерного квантования КЯ, определяемая формулой (2.5); – решение уравнения Шредингера для квантового гармонического осциллятора с нулевыми граничными условиями

,

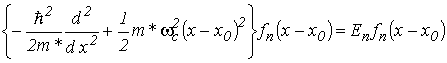где . Собственные значения энергии, соответствующие функциям (2.53), представляют собой дискретные уровни, вырожденные по квантовому числу , равные с учетом формул (2.9) и (2.52)

.

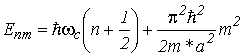(2.54)

Согласно этой формуле в поперечном магнитном поле КЯ становится аналогом квантовой точки, в которой движение ограничено по всем трем направлениям.

С учетом того, что координата точки равновесия гармонического осциллятора или центра вращения носителей заряда вокруг силовых линий магнитного поля может принимать значения в пределах ширины КЯ вдоль оси X (), компонента волнового вектора вдоль оси Y может изменяться в пределах . С учетом того, что плотность волновых векторов вдоль оси Y равна , где – ширина КЯ вдоль оси Y, степень вырождения уровня энергии (2.54), равная числу возможных значений при заданном значении индукции магнитного поля В, равна .

Наличие спина у носителей заряда приводит к дополнительной энергии их в магнитном поле, зависящей от проекции спина на вектор индукции магнитного поля. В результате этого каждый уровень энергии (2.54) расщепляется на два. Как показывает анализ, этим расщеплением по сравнению с энергетическим зазором между уровнями Ландау в большинстве случаев можно пренебречь. Тогда с учетом спина степень вырождения уровня энергии (2.54), рассчитанная на единицу площади плоскости двумерного слоя носителей заряда, будет равна

.

(2.55)

Влияние магнитного поля на физические свойства, связанные с изменением энергетического спектра и волновых функций носителей заряда, очевидно, будет иметь место для таких полей, в которых частота вращения носителей заряда вокруг силовых линий должна быть много больше частоты рассеяния, а энергетический зазор между уровнями Ландау много больше их средней энергии:

,

(2.56)

где ξ – приведенный уровень Ферми для вырожденных носителей заряда. Такие поля называются квантующими.