Теорема 3.2. (Сравните с теоремами 1.1, 2.1)

Пусть x₀ `in` Rⁿ, y₀ `in` R^m, F : О(x₀, y₀) → R^m– непрерывно дифференцируемое отображение, F (x₀, y₀) = 0,  якобиан 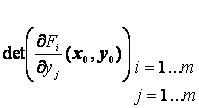не равен нулю. Тогда существуют окрестности точек x₀ и  y₀ и единственное отображение

f :О(x₀) → О(y₀ ), y₀ = f( x₀), заданное неявно системой уравнений F(x, y) = 0, причем y = f (x) непрерывно дифференцируемо и 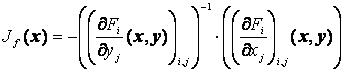  .