Теорема. Пусть Φ(x) – ограниченная функция такая, что
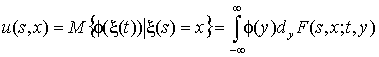 |
имеет ограниченные непрерывные производные по ξ первого и второго порядка, а коэффициенты переноса α(σ,ξ) и диффузии b(σ,ξ) являются непрерывными функциями своих аргументов. Тогда u(σ,ξ) дифференцируема по σ и удовлетворяет уравнению
![]() ,
,
а также краевому условию
![]() .
.
Следствие. Марковская переходная функция Φ(σ,ξ;t,y) удовлетворяет уравнению
![]() ,
,
которое называется обратным уравнением Колмогорова.
Если существует переходная плотность
![]() ,
,
то она также удовлетворяет обратному уравнению Колмогорова
![]() .
.
Решение этих уравнений достаточно полно определяет функционирование диффузионных процессов. Для нахождения их однозначных решений необходимо задать краевые условия, определяемые условием стохастической непрерывности в виде
для марковской переходной функции или в виде
для переходной плотности распределения.