Случайная величина ξ_ω – это измеримая функция, отображающая вероятностное пространство {Ω,F,P} на борелевскую прямую {Ω,R,B}.

Случайным процессом называют функцию ξ(ω,t), если при ∀ t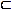T она является измеримой функцией аргумента ω, то есть случайной величиной.

Сечением случайного процесса в момент времени t будем называть случайную величину ξ_t(ω), то есть значение функции ξ(ω,t) при фиксированном значении параметра t.

Реализацией случайного процесса называют неслучайную функцию времени ξ_ω(t) при фиксированном элементарном событии ω.

Ансамбль реализаций – это совокупность всех реализаций случайного процесса.

Одномерной функцией распределения случайного процесса в момент времени t₁ называют функцию F_ξ(x₁,t₁)=P{x(t₁)<x₁}.

Двумерной функцией распределения случайного процесса для двух сечений в фиксированные моменты времени t₁ и t₂ называется функция F_ξ(x₁,t₁;x₂,t₂)=P{x(t₁)<x_1,x(t₂)<x₂}.

n-мерной функцией распределения случайного процесса для n сечений случайного процесса называется функция F_ξ(x₁,t₁;…;x_n,t_n)=P{x(t₁)<x_1,…._,x(t_n)<x_n}.

Характеристическая функция конечномерного распределения вероятностей случайного процесса определяется

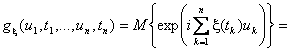
Средним значением случайного процесса ξ(t) (статистическим средним) m_ξ(t) называется математическое ожидание сечения случайного процесса в момент времени t и обозначается

.

 

Дисперсией случайного процесса ξ(t) называется дисперсия сечения случайного процесса в момент времени t

.

 

Функцией корреляции случайного процесса ξ(t) называется математическое ожидание произведения сечений случайного процесса в моменты времени t₁ и t₂

.

 

Функцией ковариации случайного процесса ξ(t) называется математическое ожидание произведения центрированных сечений случайного процесса в моменты времени t₁ и t₂

.

 

Взаимной функцией корреляции или функцией кросс-корреляции для двух случайных процессов x(t) и h(t) называется

.

 

Совместная корреляционная функция двух случайных процессов ξ(t) и η(t) определяется как матричная функция

.

 

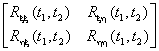Стационарным в узком смысле или строго стационарным называется случайный процесс ξ(t) при условии, что его конечномерная функция распределения инвариантна относительно сдвига всех моментов времени t_i, i=1,2,…,n на одну и ту же величину t

,

.

 

Стационарным в широком смысле называется случайный процесс, для которого среднее значение и дисперсия не зависят от времени, а функция корреляции зависит лишь от разности моментов времени.

 

Спектральная плотность S_ξ(ω) случайного процесса определяется следующим образом:

.

 

Эргодическим называется случайный процесс, для которого любая статистическая характеристика равна соответствующей характеристике, полученной усреднением по времени одной-единственной реализации.

 

Марковским называется случайный процесс ξ(t), для которого выполняется равенство

,

то есть его условная функция распределения вероятностей значений ξ(t_n+1) в будущий момент времени t_n+1 не зависит от значений процесса в прошлые моменты t₁,t₂,…,t_n-1, а определяется лишь значением ξ(t_n)=x_n в настоящий момент времени t_n.

Цепью Маркова называется марковский процесс с дискретным множеством состояний случайного процесса ξ(t).

Цепью Маркова с дискретным временем называется марковский процесс с дискретным множеством состояний X случайного процесса ξ(t) и дискретным множеством моментов времени наблюдения T.

 

Цепью Маркова с непрерывным временем называется марковский процесс с дискретным множеством состояний X случайного процесса ξ(t) и непрерывным множеством моментов времени наблюдения T.

Вероятностью перехода цепи Маркова из одного состояния в другое в момент времени t называют условные вероятности P{ξ(t´)=j|ξ(t)=i}=p_ij(t) для всех i,j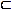X.

Матрицей вероятностей переходов цепи Маркова называют матрицу с элементами p_ij(t)=P{ξ(t´)=j|ξ(t)=i} i,j=1,2,…,n, где n – число состояний системы (число возможных значений цепи Маркова) – конечное или счетное. Элементы матрицы p_ij >0 и удовлетворяют условию нормировки

, .

 

Начальным распределением вероятностей цепи Маркова называется набор вероятностей , где , которые определяют состояние системы в начальный момент времени.

Несущественным называется состояние iX цепи Маркова, если существует такое состояние j, в которое можно попасть с положительной вероятностью, но из которого нельзя вернуться в i, то есть

$ m, j , .

 

Состояние j называется достижимым из состояния i (обозначается i®j), если $ n>0, что p_ij⁽ⁿ⁾>0.

Состояния i и j называются сообщающимися (обозначается i«j), если j достижимо из i и i достижимо из j.

Множества X₁,X₂…, состоящих из сообщающихся состояний и характеризующихся тем, что переходы между различными множествами невозможны, называются замкнутыми классами или неразложимыми классами, существенных сообщающихся состояний.

Цепь Маркова называется неразложимой, если ее состояния образуют один неразложимый класс.

Периодом замкнутого класса d(j) называют наибольший общий делитель чисел n таких, что p_jj(n)>0.

 

Апериодическим (эргодическим) называется состояние j (класс X), для которого период равен единице d(j)=1, (d(X)=1).

Возвратным называется состояние iX, если вероятность того, что система, выйдя из состояния i, хотя бы один раз вернется в него, равна 1, то есть , где  f_i(n) – вероятность первого возвращения в состояние i на n-м шаге.

 

Финальным или эргодическим называется распределение вероятностей p_i определяемых как , где и однозначно определяется условиями:

– уравнением Колмогорова для финальных вероятностей,

– условием нормировки для финальных вероятностей.

 

Вероятностью перехода p_ij(s,t) из состояния i в состояние j за промежуток времени [s,t) для цепи Маркова с непрерывным временем называется

для любых i´, i, jÎX и s´< s < t ÎT.

 

Однородной называется цепь Маркова, если вероятности переходов p_ij(s,t) зависят только от разности моментов времени, то есть p_ij(s,t)=p_ij(t–s)=p_ij(t).

 

Инфинитезимальными характеристиками цепи Маркова с непрерывным временем называют величины

,

.

 

Случайным потоком однородных событий называется последовательность t₁<t₂<…<t_n моментов наступления событий за время t. П

Стационарным называется поток, если число событий, наступивших на интервале [s,t), не зависит от положения этого интервала на оси времени, а определяется лишь его длиной t–s.

Потоком без последействия называется поток, если число событий, наступивших на некотором интервале времени, не зависит от числа событий, наступивших на других, не пересекающихся с ним, интервалах.

Ординарным потоком называется поток, для которого вероятность наступления более одного события за бесконечно малый промежуток времени является бесконечно малой более высокого порядка, чем длина рассматриваемого промежутка.

Простейшим называется поток однородных событий, удовлетворяющий свойствам ординарности, стационарности и отсутствия последействия.

Производящей функцией случайного процесса i(t) называется функция

, где P_m(t)=P{i(t)=m}.

 

Непрерывным марковским процессом называется случайный процесс ξ(t) если для любых моментов времени s ׳ <s<t ÎT и любых действительных y выполнено равенство

.

 

Марковской переходной функцией называется условная функция распределения

.

 

Диффузионным называется непрерывный марковский процесс, если его марковская переходная функция удовлетворяет следующим условиям:

1. Для ∀ε>0 и любых x равномерно по s<t выполняется предельное равенство

.

Это условие требует, чтобы вероятность того, что  |ξ(t)–ξ(s)|>ε, была бы величиной бесконечно малой более высокого порядка малости, чем |t–s|, при t→s.

2. Существуют функции  a(s,x) и b(s,x) такие, что

,

,

здесь функция a(s,x) называется коэффициентом переноса, а функция b(s,x) – коэффициентом диффузии.

3. Для любых k>2

.

 

Диффузионный процесс авторегрессии – диффузионный процесс, для которого коэффициенты переноса и диффузии имеют вид a(y)=–ay, b(y)=s2.

Винеровским диффузионным процессом называют однородный диффузионный процесс с коэффициентами переноса и диффузии вида a(y)=0 b(y)=s².