Для успешного изучения методов многомерной статистики необходимы знания в таких областях высшей математики как аналитическая геометрия, матричная алгебра, многомерный математический анализ. Практически все методы многомерной статистики условно можно разбить на две группы, представленные на схеме (рис.1.1.).

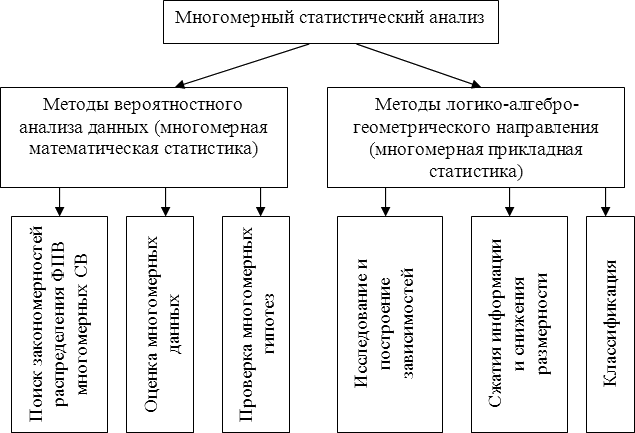Рис. 1.1. Схема методов математической и прикладной статистики. ФПВ - функция плотности вероятностей случайной величины (СВ) (Горелова, Кацко, 2005)

В данном учебном пособии рассматриваются только методы многомерной прикладной статистики. Эту группу методов ещё называют многомерный статистический анализ данных. Характерной особенностью этих методов является геометрическое представление данных. Наблюдаемые объекты можно изобразить как точки в n-мерном пространстве, соответствующем числу признаков, которыми они характеризуются. Если признаки разнородны, то их нормируют.

Назначение методов многомерного статистического анализа данных не является однозначным. Например, задачи группирования объектов по принципу сходства признаков можно осуществлять и кластерным и факторным анализом. У каждого метода есть свои сильные и слабые стороны. Ниже приводится краткая сравнительная характеристика основных методов многомерного статистического анализа данных, рассматриваемых в данном учебном пособии.