Основные типы представления многомерных данных Все статистические пакеты обрабатывают информацию, представленную в виде одного из трёх типов: матрицы данных, матрицы мер близостей (расстояний), матрицы связей (между переменными). Каждая из этих матриц может являться входной матрицей, либо возникать как результат работы программ обработки. Такое деление данных носит в первую очередь содержательный характер, файлы для хранения и ввода этих данных имеют одинаковую логическую организацию, отличаясь лишь содержимым.

Матрица данных. Эта матрица, задающая отношение "объект-признак ", является одной из наиболее частых форм организации данных и представляет собой двумерную таблицу размера n x m

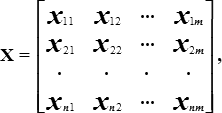
где каждая строка - новый объект, значения в строке - характеристики свойств объекта (признаки) или, по математической терминологии, векnор-строка [X_i] = {x_i1, x_i2 ,…, x_im} является совокупностью значений m признаков, измеренных у i-го объекта. В дальнейшем наряду с термином признак будем употреблять также термины переменная.

Матрица связи между признаками. Эта матрица задаёт отношение "признак-признак" и представляет собой двумерную симметричную квадратную матрицу размера m х m:

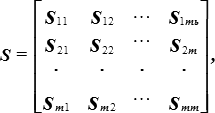
где S_ij может быть либо коэффициентом корреляции (ковариации) между i- м и j-м признаками, либо какой-либо другой мерой связи между признаками. Наиболее часто в качестве матрицы связи "признак-признак" используется ковариационная матрица, которая наряду с векторами средних значений признаков является основным промежуточным звеном для методов сокращения размерности, регрессии, дискриминантного анализа, основанных на линейных моделях. Диагональный элемент этой матрицы представляет собой оценку дисперсии признака x_j, которая характеризует степень рассеивания значений этого признака относительно среднего.

Матрица близостей (удаленностей расстояний). Эта матрица, задающая отношение "объект-объект" представляет собой квадратную симметричную матрицу размера n x n c неотрицательными элементами:

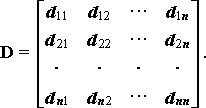
Элемент d_ij является значением некоторой меры близости (удалённости) между объектами x_i и x_j. Диагональные элементы этой матрицы значения не имеют, так как в последующей обработке матрицы не используются. Если элемент матрицы вычисляется как расстояние между двумя объектами, то матрица [D] отражает геометрическую конфигурацию точек (объектов) в m-мерном пространстве признаков. Матрица расстояний (близостей) между объектами, как правило, вычисляется по матрице [Х] и применяется в процедурах кластер-анализа или метрического шкалирования.