Влияние размерного квантования на проводимость КН особенно ярко проявляется при наличии баллистического переноса, т.е. при условии того, что длина L квантовой нити меньше, чем длина свободного пробега носителей заряда [1].
|
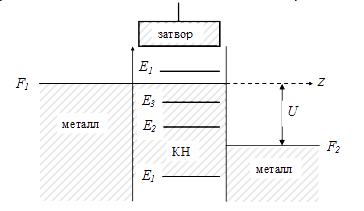
Рис. 5.4. Энергетическая диаграмма смещенной структуры с КН при наличие затвора |
Чтобы описать баллистический перенос, рассмотрим протекание тока через КН между двумя металлическими контактами с вырожденным электронным газом, на которые подано напряжение U. Согласно рис. 5.4 электрический ток в такой структуре создается за счет баллистического перехода электронов с энергией ![]() из левого контакта в правый. Величина тока, создаваемого этими электронами с учетом вырождения и формулы (2.20) – дисперсии энергии по волновому вектору вдоль оси КН – равна
из левого контакта в правый. Величина тока, создаваемого этими электронами с учетом вырождения и формулы (2.20) – дисперсии энергии по волновому вектору вдоль оси КН – равна
| (5.57) |
где 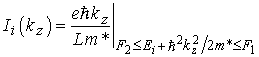
– ток, создаваемый электроном подзоны с номером i и компонентой волнового вектора kz. С учетом квазинепрерывности волнового вектора расчет силы тока по формуле (5.57) приводит к следующему выражению:
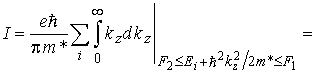
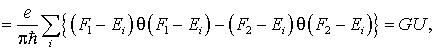
где ![]() – функция Хевисайда (3.3). Если смещение невелико относительно промежутков энергии между подзонами, т. е. выполняется условие
– функция Хевисайда (3.3). Если смещение невелико относительно промежутков энергии между подзонами, т. е. выполняется условие
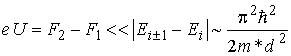 ,
,
где d – средний диаметр КН, формула для баллистической проводимости принимает простой вид
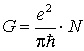 . . |
(5.58) |
В этой формуле N – число подзон, содержащих электроны, т.е. дно которых лежит ниже уровня Ферми F2. Полученная формула носит общий характер и, кроме мировых констант, не зависит ни от характеристик нити (за исключением числа заполненных подзон), ни от условий измерений. Согласно этой формуле баллистическая проводимость КН может принимать только определенные значения, кратные выражению из мировых констант e и ![]() , т.е. является квантованной величиной. Скачкообразный – квантованный характер зависимости баллистической проводимости как функции числа заполненных подзон можно наблюдать в структурах с КН, изменяя концентрацию носителей заряда с помощью напряжения, прикладываемого к затвору Шоттки (рис. 5.5). По мере уменьшения отрицательного потенциала на затворе концентрация электронов в ней возрастает. При этом растет число заполненных подзон как за счет понижения дна этих подзон относительно уровня Ферми в контактах, так и за счет уменьшения энергетического зазора между подзонами [1].
, т.е. является квантованной величиной. Скачкообразный – квантованный характер зависимости баллистической проводимости как функции числа заполненных подзон можно наблюдать в структурах с КН, изменяя концентрацию носителей заряда с помощью напряжения, прикладываемого к затвору Шоттки (рис. 5.5). По мере уменьшения отрицательного потенциала на затворе концентрация электронов в ней возрастает. При этом растет число заполненных подзон как за счет понижения дна этих подзон относительно уровня Ферми в контактах, так и за счет уменьшения энергетического зазора между подзонами [1].
|
Рис. 5.5. Экспериментальная зависимость проводимости КН (точечного контакта) от напряжения на затворе, определяющего концентрацию носителей [1] |
Согласно формуле (5.58) баллистическое сопротивление КН не зависит от ее длины и сечения. В одноподзонном приближении значение ее сопротивления является универсальной величиной [9]:
![]() .
.
Экспериментальные исследования квантования проводимости в коротких (баллистических) нитях часто проводятся на структурах, представляющих собой, строго говоря, не нить как таковую, а так называемый точечный контакт, т.е. узкую перемычку, соединяющую собой два участка двумерного электронного газа достаточно большой площади. Формально это как бы нить, имеющая длину, сравнимую с ее шириной, причем последняя имеет достаточно малую величину. Квантование проводимости должно наблюдаться и в таких структурах (это неудивительно, поскольку окончательная формула (5.58) не содержит никаких конкретных параметров, описывающих размеры и форму нити). В частности, экспериментальная зависимость, показанная на рис. 5.5, получена именно на таком квантовом микроконтакте [1].
Одним из основных применений квантования баллистической проводимости КН является калибровка высокоточных приборов электротехники, используемых в научных исследованиях.