Для того, чтобы облегчить выписывание уравнений (6), обыкновенно вводят вспомогательную функцию 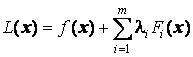, которая называется функцией Лагранжа. Для этой функции первые  m + n уравнений системы (5.6) выглядят как необходимое условие ее экстремума, то есть dL(x₁,..., x_{n + m}, λ₁, ..., λ_m) = 0. Действительно:

 

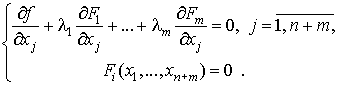    (6)

Отметим, что в системе (6) нет разницы между зависимыми и независимыми переменными.

Перейдем теперь к достаточным условиям экстремума. Предположим существование и непрерывность вторых производных для функций f, F_i , i = 1, ..., m. Пусть теперь точка M₀ и множители λ_i , i = 1, ..., m удовлетворяют установленным выше необходимым условиям. Вопрос о наличии в этой точке условного экстремума зависит от знака Δf (M₀):

Δf(M₀) = f(M) – f(M₀) ,

где координаты точки M удовлетворяют условиям связи: Тогда

.

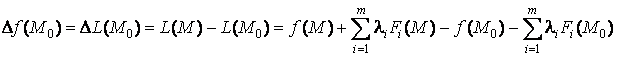Чтобы удовлетворить достаточным условиям экстремума, для функции Лагранжа найдем

.

 

Заметим, что в критической точке M₀ все частные производные  первого порядка от функции L равны нулю, поэтому

.

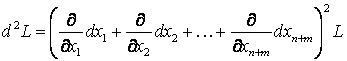Иногда для исследования знака квадратичной формы d²L требуется использовать систему (4). Такая ситуация возникает, если получившийся второй дифференциал d²L является нестрого определённой квадратичной формой.