Наибольший интерес представляет случай, когда  переменные x_n+1,..., x_n+m не могут быть явно выражены через функции φ₁(x₁,x₂,...,x_n), ..., φ_m(x₁,x₂,...,x_n) . Рассмотрим его подробнее.

          Если в точке M₀ функция  имеет условный экстремум, то её дифференциал тождественно относительно дифференциалов начальных переменных обращается в нуль. Найдем df(M₀), используя свойство инвариантности дифференциала первого порядка:

,                                        (3)

где dx_n+1,..., dx_n+m есть дифференциалы неявно заданных условиями связи функций переменных x₁,x₂,..., x_n. В (5.3) мы не можем положить равными нулю коэффициенты при дифференциалах, ибо не все дифференциалы являются независимыми. Продифференцируем условия связи полным образом:

                                                              (4)

          Систему (4) можно рассматривать как систему неоднородных линейных уравнений для определения дифференциалов dx_n+1,..., dx_n+m :

 

 Определитель этой системы представляет собой якобиан  (см. (2)). Разрешая эту систему относительно dx_n+1,..., dx_n+m  и подставляя найденные дифференциалы зависимых переменных в (4), получим:, где A₁,..., A_n обозначают n  выражений, рациональных относительно частных производных функций F_i , i = 1,..., m , вычисленных в точке M₀. Так как в этом равенстве имеются только дифференциалы независимых переменных, то в точке M₀ имеем A_i = 0, i = 1,..., n. Присоединяя к ним m условий связи, получим n + m уравнений для определения точек возможного экстремума.

          В рассмотренном методе есть существенный недостаток:  переменные неравноправны (одни из них трактуются как независимые, другие от них зависят). Лагранжем был придуман очень остроумный метод, в котором этот недостаток отсутствует. Сначала все-таки будем считать, что переменные x₁,x₂,..., x_n независимы, а остальные от них зависят. Умножим равенства (4) на неизвестные пока числовые коэффициенты λ₁, ..., λ_m и сложим с равенством (3), получим

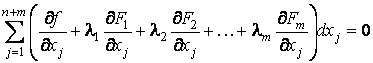                               .                   (5)

Положим теперь коэффициенты при зависимых дифференциалах dx_n+1,..., dx_n+m равными нулю: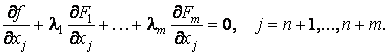

 

Будем рассматривать полученную систему как систему линейных неоднородных уравнений для определения числовых коэффициентов λ₁, ..., λ_m . Эта система имеет единственное решение, ибо ее определитель есть отличный от нуля якобиан . Но тогда в (5) останутся лишь независимые дифференциалы, а значит, коэффициенты при них должны быть равны нулю:

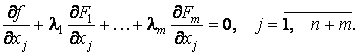
      Итак, для определения точек возможного экстремума имеем  n + 2m уравнений

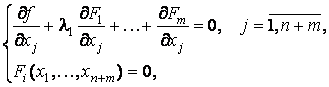                                                            (6)

из которых определяем n + 2m неизвестных