Пусть аргументы функции U = f(x₁,x₂,...,x_n+m) связаны соотношениями:

F_i(x₁,x₂,...,x_n+m) = 0,  i = 1, ..., m ,                                  (1)

которые называются уравнениями связи.

Определение. Точка M₀, удовлетворяющая уравнениям связи, называется точкой условного максимума [минимума] функции f(x₁,x₂,...,x_n), если неравенство f (x₁,x₂,...,x_n+m) ≥  f (M₀) [ f (x₁,x₂,...,x_n+m) ≤  f (M₀)]

выполняется в некоторой окрестности точки M₀ для всех точек x = (x₁,x₂,...,x_n+m), удовлетворяющих уравнениям связи.

Будем предполагать, что функция  f и функции F_i имеют в окрестности рассматриваемой точки непрерывные частные производные по всем аргументам. Пусть  в точке M₀ отличен от нуля хотя бы один определитель m-го порядка, составленный из матрицы частных производных отображения F = F₁i₁+...+F_mi_m, например определитель

.              (2)

Тогда, если ограничиться достаточно малой окрестностью точки  M₀, система (5.1) (согласно теореме о неявном отображении, теорема 3.2) равносильна системе вида , где φ₁, ..., φ_m есть неявные функции, определяемые системой (1). Таким образом, вопрос об условном экстремуме функции f (x₁,x₂,..., x_n +m) в точке M₀ сводится к обыкновенному экстремуму сложной функции

f(x₁,x₂,..., x_n , φ₁(x₁,x₂,...,x_n), ..., φ_m(x₁,x₂,...,x_n) ) в точке .

Пример 5.1. Исследовать на экстремум функцию z = x²+y² при условии x + y = 4.

Решение. Разрешим уравнение связи относительно одной из переменных, например, относительно y: y = 4 – x.

При найденном y функция  z становится функцией одной переменной: z =

Исследуем эту функцию на экстремум. Для этого находим критические точки по первой производной: . Проверяем достаточное условие экстремума, то есть смену знака производной функции z(x):

 

Таким образом, в точке x₀ = 2 функция z(x) имеет минимум, равный 8.

Это означает, что функция z = x²+y² имеет условный минимум при y = 4 – x в точке (2; 2).

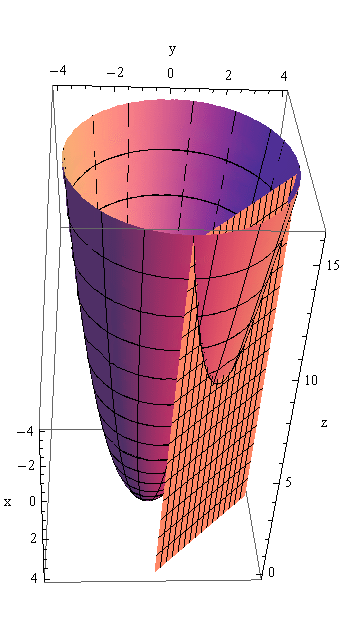
C точки зрения графика этот результат означает следующее: график функции z = x² + y² (параболоид) пересекается с поверхностью x + y = 4 (плоскость). В результате получается парабола, минимум которой (по оси z) и требуется найти.