Пример 2.3. Найти локальные экстремумы каждой непрерывно дифференцируемой функции z = f(x,y), заданной неявно равенством (x²+y²)²+z⁴–8(x²+y²)–10z²+16 = 0.

 

 

Применим теорему 2.1, чтобы узнать, в окрестностях каких точек (x, y, z) неявная функция z = f(x, y) определена. Здесь вмести переменной y нужно рассмотреть z, так как именно переменную z требуется сделать функцией. Роль переменной x(x₁, ..., x_n) выполняет (x, y) `in R`² . Основное условие, которое должно выполнятся в таких точках: Имеем при  .

 

Это означает: если точка (x,y,z) удовлетворяет уравнению (x²+y²)²+z⁴–8(x²+y²)–10z²+16 = 0 и  , то в такой точке неявная функция z = f(x,y) определена и единственна.

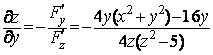Найдём частные производные функции z = f(x,y) по формуле, указанной в теореме 2.1:

,  . (1)

Приравнивая эти производные к нулю, приходим к системе: .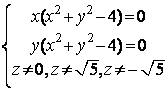

Решая эту систему, находим критические точки:

x_{1, 2, 3, 4}= 0, y_{1, 2, 3, 4} = 0, z⁴–10z²+16 = 0 => ;

x_{5, 6}=0, y₅= 2, y₆= –2, 16+z⁴–32–10z²+16 = 0 => z²(z²–10)=0, ;

y_{7, 8}=0, x₇= 2, x₈= –2, 16+z⁴–32–10z²+16 = 0 => z²(z²–10)=0, .

Вообще, при x²+y²=4 получаем , то есть экстремумы в таких точках если и есть, то нестрогие. Таким образом, нужно проверить наличие экстремума в первых четырёх точках.