Теорема 3.1. 1. Пусть x₀ `in` Rⁿ, f: О(x₀) → R^m, y₀ `in` R^m, y₀=f(x₀), g : О(y₀) → R^k. Тогда .

2. Пусть x₀ `in` R^m, f: О(x₀) →Y – биекция (Y `sub` R^m), y₀ = f (x₀). Тогда .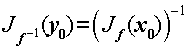

Пример 3.2. Пусть f (x₁, x₂) = (x₁· x₂, x₁/x₂). Определим обратное отображение к f.

Если y₁= x₁· x₂, y₂= x₁/x₂, то x₁= y₁/ x₂ , y₂= y₁/(x₂)², откуда при x₂ > 0 имеем

x₂= (y₁/y₂)^1/2, x₁= (y₁· y₂)^1/2.

Отображение f будет биекцией, например, если f: G_x → G_y,

где G_x={( x₁, x₂)`in` R²: x₁ > 0, x₂ > 0}, G_y={( y₁, y₂)`in` y₁ > 0, y₂ > 0}. Обозначим g = f ^–1.

Тогда g(y₁, y₂)=f^­ –1(y₁, y₂) = ((y₁· y₂)^1/2, (y₁/y₂)^1/2),

J_f–1(y) =,   .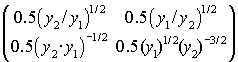

Якобиан обратного отображения можно было получить, используя теорему о свойствах матрицы Якоби, п.2. А именно, из раздела 2 следует, что =  (–2 x₁/x₂)^–1= –1/(2y₂) (см. пример 3.1).