В случае, когда один из игроков имеет всего две чистые стратегии, решение игры может быть получено с помощью графического способа. В основе этого способа лежат соотношения (4.8) и (4.9) теоремы Неймана. Приведем схему реализации графического способа для матричной игры размера . Она состоит в выполнении двух шагов.

      Шаг 1. В декартовой системе координат строятся графики функций , выражающих средний выигрыш игрока G₁ на своей см.-стратегии  в ответ на чистую стратегию  игрока G₂:

,().

(4.14)

Формулы (4.14) определяют отрезки прямых (рис. 4.1).

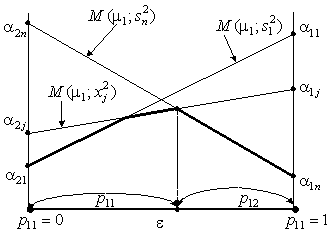
Рис. 4.1. Графический способ решения антагонистической игры размера

      Шаг 2. Ищется максимум нижней огибающей всего семейства построенных на шаге 1 отрезков (жирная линия на рис. 4.1). Точка максимума  и определяет искомую равновесную см.-стратегию

 

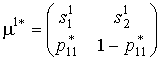
для игрока G₁. Значение максимума огибающей определяет значение цены игры  в см.-стратегиях.

      Шаг 3. Из графического построения выясняется, результатом пересечения каких отрезков является точка максимума огибающей. Номера этих отрезков фиксируются (допустим, этими отрезками являются отрезки с номерами i и  k, соответствующие стратегиям  и  игрока G₂).

      Аналогично проводится решение для игры .