Рассмотрим антагонистическую игру  в нормальной форме с платежной матрицей . Пусть  и  – произвольные см.-стратегии игроков G₁ и G₂ соответственно. Тогда средний выигрыш игрока G₁ в ситуации см.-стратегий  определится как

.

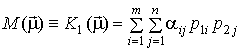(4.4)

Число

(4.5)

называется нижней ценой игры в классе см.-стратегий. Это число является, посути, средним значением гарантированного выигрыша игрока G₁. См.-стратегия , при которой достигается значение нижней цены l игры в классе см.-стратегий, называется защитной см.-стратегией игрока G₁.

(4.6)

называется верхней ценой игры в классе см.-стратегий. Это число является, посути, средним значением гарантированного проигрыша игрока G₂. См.-стратегия , при которой достигается значение верхней цены u игры в классе см.-стратегий, называется защитной см.-стратегией игрока G₂.

      Пара  см.-стратегий называется уравновешенной, если для любых ,  справедливо  . Величина  называется ценой (значением) игры  в классе см.-стратегий.

      Теорема о защитности см.-уравновешенных стратегий. Пара см.-стратегий уравновешена тогда и только тогда, когда она является парой защитных см.-стратегий.

            Теорема Неймана. Любая конечная антагонистическая игра имеет решение  в см.-стратегиях. При этом справедливы соотношения

,

(4.7)

,

(4.8)

.

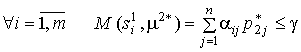(4.9)