Интерполяцию векторных величин проводят следующим образом: векторная величина представляется в алгебраической форма, т.е. как набор компонент, которые рассматриваются как неизвестные скалярные величины. Каждый узел содержит n неизвестных, где n – размерность пространства.

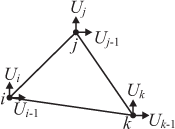
Используемое обозначение компонент вектора, проиллюстрировано для одно-, двух- и трехмерного случаев, показано на рис. 11,


а	б

Рис. 11. Обозначения узловых векторных величин, используемые в снмплекс-элементах: а – одномерный элемент; б – двухмерный элемент

где все компоненты обозначаются буквой U, отдельные компоненты различаются нижним индексом, а числовые значения нижних индексов упорядочиваются в соответствии с направлением компонент вектора по осям x, y.

В одномерной задаче представление векторной величины внутри элемента совпадает с представлением скалярной величины (6). В двухмерном случае при рассмотрении векторной величины имеем

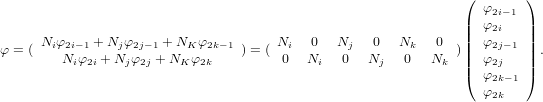( φ2i−1 ) | φ2i | Niφ2i−1 + Njφ2j−1 + NK φ2k−1 Ni 0 Nj 0 Nk 0 || φ2j−1 || φ = ( Ni φ2i + Njφ2j + NK φ2k ) = ( 0 Ni 0 Nj 0 Nk )|| φ2j || . |( φ2k−1 |) φ2k

(10)

Очевидно, что трехмерный случай является аналогичным.

Особые свойства полиномов (3), (7) позволяют использовать их для аппроксимации величии внутри элемента. Они дают правильные результаты, когда узловые значения рассматриваемых величин равны между собой, и обеспечивают непрерывность в межэлементных зонах. Таким образом, сходимость решения, полученного методом конечных элементов, будет увеличиваться с уменьшением размеров элемента (если узловые значения оказываются равными между собой), когда интерполяционные уравнения приводят к постоянным значениям рассматриваемых величин внутри элемента, а градиенты бесконечно малы. Необходимым условием постоянства значений рассматриваемых величин внутри элемента является

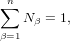∑n Nβ = 1, β=1

(11)

т.е. сумма значений функций формы должна равняться единице и каждой внутренней точке элемента. Здесь n – число узлов. Анализируя представленные выше симплекс-элементы, можно показать, что функции формы для этих элементов удовлетворяют условию (11), а градиенты асимптотически стремятся к нулю если удовлетворяется (11).

Дискретная модель для непрерывной функции строится на множестве кусочно-непрерывных функций, каждая из которых, определена на отдельном элементе. Очевидно, что интеграл от функции, определенной на каждом элементе, ограничен. Чтобы интеграл был ограничен на множестве кусочно-непрерывных функций, необходимо провести процедуру сшивания на границах каждого элемента. Эта процедура для соответствующих полиномов имеет четкую структуру с наличием алгоритма и реализована в COMSOL, алгоритм реализации можно посмотреть в Help и указанных там ссылках.