Самыми распространенными функциями, которые используются для аппроксимации непрерывной функции дискретной моделью в методе конечных элементов, являются полиномы. Они строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых элементами. Порядок полинома зависит от числа используемых в каждом узле элемента данных о непрерывной функции. Классификация конечных элементов может быть проведена в соответствии с порядком полиномиальных функций этих элементов. При этом рассматриваются три следующие группы элементов: симплекс-, комплекс- и мультиплекс-элсменты.

Симплекс-элементам соответствуют полиномы, содержащие константу и линейные члены, в которых число коэффициентов на единицу больше размерности координатного пространства. Например, полином

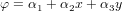φ = α1 + α2x + α3y

(1)

представляет собой симплексную функцию для двухмерного треугольного элемента (рис. 2а), является линейным по x, y и содержит три коэффициента, которые определяются из условий для узлов треугольника.

Комплекс-элементы являются расширением класса симплекс-элементов. В них могут присутствовать не только линейные слагаемые, но и члены второго, третьего и более высокого порядка.

Форма комплекс-элементов может быть такой же, как и у симплекс-элементов, но комплекс-элементы имеют дополнительные граничные узлы и могут иметь внутренние узлы. Главное различие между симплекс- и комплекс-элементами состоит в том, что число узлов в комплекс-элементе больше величины, равной размерности координатного пространства плюс единица. Интерполяционный полином для двухмерного треугольного комплекс-элемента (рис. 2б) имеет вид

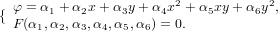2 2 { φ = α1 + α2x+ α3y + α4x + α5xy +α6y , F (α1,α2,α3,α4,α5,α6) = 0.

(2)

Это соотношение включает пять независимых коэффициентов, так как рассматриваемый элемент должен имеет пять узлов.

Мультиплекс-элементы также содержат члены высокого порядка, но границы элементов при этом должны быть параллельны координатным осям, что необходимо для достижения непрерывности при переходе от одного элемента к другому. Это требование является достаточно сильным, поэтому мультиплекс-элементы имеет смысл использовать в сильно ограниченном круге задач.

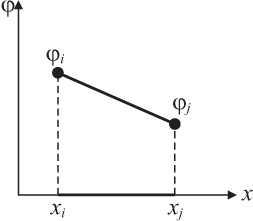
Рассмотрим одномерный симплекс-элемент, представляющий собой прямолинейный отрезок длины L с двумя узлами (рис. 9), и обозначим эти узлы индексами i и j, узловые значения φ_i, и φ_j – соответственно.

Рис. 9. Одномерный элемент с двумя узлами, который аппроксимируется простейшим полиномом

Начало системы координат располагается вне элемента. Полиномиальная функция φ имеет вид

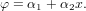φ = α +α x. 1 2

(3)

Используя условия в узловых точках φ(x_i) = φ_i и φ(x_j) = φ_j, можно найти коэффициенты α₁ и α₂:

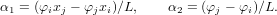α1 = (φixj − φjxi)∕L, α2 = (φj − φi)∕L.

(4)

Подставляя (4) в (3), получим

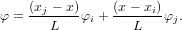φ = (xj −-x)φi + (x−-xi)φj. L L

(5)

Линейные функции от x в (5) называются функциями формы, или интерполяционными функциями. Каждая функция формы должна быть снабжена нижним индексом для обозначения узла, к которому она относится. Обозначим N_i = (x_j − x)∕L и N_j = (x_i − x)∕L, тогда выражение (5) будет иметь вид

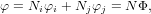φ = Niφi + Njφj = N Φ,

(6)

где N = (N_i,N_j) – матричная строка, а

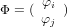$φ Φ = ( φi ) j$ – вектор-столбец. Очевидно, что функция N_i равна единице в узле с номером i и равна нулю в узле j, а функция N_j наоборот. Эти значения характерны для функций формы. Они равны единице в одном определенном узле и обращаются в нуль во всех других узлах.

В качестве примера двухмерного симплекс-элемента выберем треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине (рис. 10).

Рис. 10. Двухмерный треугольный элемент с тремя узлами. Здесь узловые значения скалярной величины φ обозначены через φ_i, φ_j, и φ_k, а координатные пары (x_i,y_i), (x_j,y_j), (x_k,y_k)

Нумерацию узлов элемента осуществим последовательно против часовой стрелки, начиная от некоторого i-го узла, который выбирается произвольно.

Интерполяционный полином имеет вид

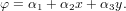φ = α + α x+ α y. 1 2 3

(7)

Используя условия в узловых точках φ(x_i,y_i) = φ_i, φ(x_j,y_j) = φ_j и φ(x_k,y_k) = φ_k, можно найти коэффициенты α₁, α₂ и α₃:

α1 = [(xjyk − xkyj)φi + (xkyi − xiyk)φj + (xiyj − xjyi)φk ]∕(2S), α2 = [(yj − yk)φi + (yk − yi)φj + (yi − yj)φk]∕(2S ), (8) α3 = [(xk − xj)φi + (xi − xk)φj + (xj − xi)φk]∕(2S ),

где S – площадь треугольника.

Проводя процедуру, аналогичную одномерному случаю, получим элемент, содержащий три функции формы:

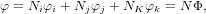φ = Niφi + Nj φj + NK φk = NΦ,

(9)

где

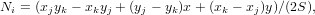
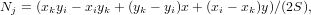
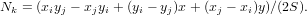$Ni = (xjyk − xkyj + (yj − yk)x+ (xk − xj)y)∕(2S),$ $Nj = (xkyi − xiyk + (yk − yi)x+ (xi − xk)y)∕(2S),$ $Nk = (xiyj − xjyi +(yi − yj)x+ (xj − xi)y)∕(2S).$ Проведя тривиальные вычисления, получим, что, аналогично одномерному случаю, функция N_i равна единице в узле с номером i и равна нулю в остальных узлах и во всех точках прямой, проведенной через эти узлы.

Скалярная величина φ определяется внутри элемента функциями формы, линейной по x и y. Это означает, что необходимо использовать очень малые по величине элементы, чтобы аппроксимировать быстро меняющуюся функцию φ.

Расширение на трехмерный случай осуществляется аналогичным образом.