При непрерывном начислении процентов полагают, что количество периодов начисления процентов в году m → ∞. Формула наращенной суммы при непрерывном начислении процентов имеет вид

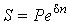где P – исходная сумма; S – наращенная сумма; δ – сила роста (ставка непрерывных процентов); n – срок операции в годах; e^δn – множитель наращения непрерывных процентов.

Пример 9.

Банковский вклад предполагает непрерывное начисление процентов с силой роста 5 % годовых. Клиент внес 250 тыс. руб. на 9 месяцев. Определите наращенную сумму вклада.

Решение. P = 250 000; δ = 0,05; n = 9/12 (= 0,75). По формуле непрерывных процентов получаем наращенную сумму

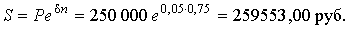Если сила роста изменяется во времени, то формула непрерывных процентов имеет вид

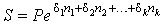где δ₁, δ₂, …, δ_k – силы роста, действующие в периодах n₁, n₂, …, n_k, следующих друг за другом (n₁ + … + n_k = n).

Пример 10.

Договор предусматривает непрерывное начисление процентов на сумму 50 тыс. руб. Сила роста изменяется дискретно: первые два года проценты начисляются по ставке 8 %, следующие 3 года – 9 % и далее в течение 5 лет – 10 %. Определите наращенную сумму.

Решение. P = 50 000; n = 10. Срок операции разбит на 3 периода:

1) δ₁ = 0,08; n₁ = 2;

2) δ₂ = 0,09; n₂ = 3;

3) δ₃ = 0,1; n₃ = 5.

Используя формулу непрерывных процентов с переменной силой роста, получаем

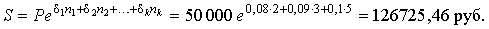При непрерывном изменении силы роста

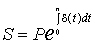где t – время; δ = δ(t) – непрерывная функция, описывающая динамику величины силы роста во времени.

Пример 11.

Вклад в размере 300 000 руб. открыт на 5 лет с непрерывным начислением процентов. Сила роста изменяется с постоянным годовым темпом роста 1,2; ее начальное значение – 15 % годовых. Определите наращенную сумму вклада к концу его срока.

Решение. P = 300 000; n = 5. Сила роста изменяется во времени, эти изменения можно описать непрерывной функцией

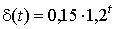при этом δ(0) = 0,15; δ(1) = 0,15∙1,2; δ(2) = 0,15∙1,2² и т.д. Вычислим

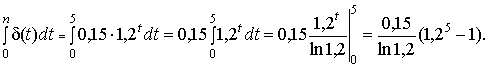Наращенная сумма будет равна

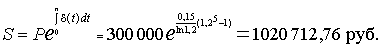В практических финансовых операциях непрерывные процессы наращения денежных сумм, т.е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном анализе сложных финансовых задач, например при обосновании и выборе инвестиционных решений. Это связано с тем, что многие экономические процессы по своей природе непрерывны, поэтому при их описании более адекватно применение непрерывных процентов. Модели с непрерывными процентами широко используют в современной финансовой математике при описании доходностей ценных бумаг. С помощью непрерывных процентов можно учесть сложные процессы наращения, часто изменяющиеся процентные ставки, что характерно для финансовых рынков.