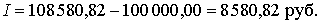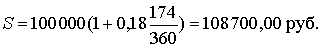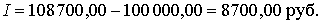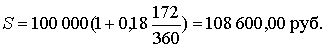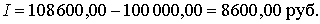При начислении простых процентов базой для начисления служит исходная сумма денег на протяжении всего срока финансовой операции. В этом случае говорят, что используется простая процентная ставка.

Формула наращения по простым процентам имеет вид

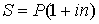где P – исходная сумма денег; S – наращенная сумма; i – годовая ставка простых процентов; n – срок операции, выраженный в годах; (1 + in) – множитель наращения простых процентов.

Проценты за весь срок операции определяют по формуле

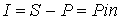Пример 1.

Ссуда в размере 5 000 руб. выдана на три года под простую процентную ставку 20 % годовых. Определите проценты и сумму, подлежащую возврату.

Решение. P = 5 000; i = 0,2; n = 3. По формуле простых процентов получаем наращенную сумму долга

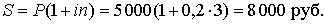Сумма начисленных процентов

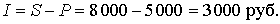Ответ: через три года необходимо вернуть общую сумму в размере 8 000 руб., из которой 5 000 руб. составляет основной долг, а 3 000 руб. – проценты (по 1 000 руб. в год).

Если срок финансовой операции n не равен целому числу лет (например, когда продолжительность операции менее года), то его представляют в виде дроби. Если срок выражен в месяцах, то

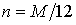где M – срок операции в месяцах.

Если срок выражен в днях, то

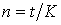где t – срок операции в днях; K – временная база.

В расчетах используют два типа временных баз: K = 360 – обыкновенные проценты, K = 365(366) – точные проценты. Число дней операции также может быть определено точно (по календарю) или приближенно (из расчета, что в каждом месяце ровно 30 дней).

В связи с этими различиями существуют три метода расчета простых процентов:

• точные проценты с точным числом дней операции (английский метод, обозначается 365/365);
• обыкновенные проценты с точным числом дней операции (французский метод, обозначается 365/360);
• обыкновенные проценты с приближенным числом дней операции (германский метод, обозначается 360/360).

Даты начала и окончания операции во всех случаях считаются за один день.

Пример 2.

Ссуда в размере 100 тыс. руб. выдана 10 октября под 18 % годовых. Определите размер погасительного платежа на 2 апреля следующего года (год не високосный):

а) по точным процентам с точным числом дней ссуды (365/365);

б) по обыкновенным процентам с точным числом дней ссуды (365/360);

в) по обыкновенным процентам с приближенным числом дней ссуды (360/360).

Оцените, какой метод расчета процентов выгоден банку, а какой заемщику, и почему.

Решение. P = 100 000; i = 0,18. Определим число дней ссуды: точное – 174 (= 22+30+31+31+28+31+2–1), приближенное – 172 (= 21+30∙5+2–1). Формула расчета погасительного платежа: 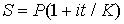, процентов: .

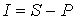а) Точные проценты с точным числом дней ссуды (365/365):

t = 174, K = 365: ,

б) Обыкновенные проценты с точным числом дней ссуды (365/360):

t = 174, K = 360:

в) Обыкновенные проценты с приближенным числом дней ссуды (360/360):

t = 172, K = 360:

Банку будет выгоднее начислять проценты методом 365/360, позволяющим получить максимальный процентный доход 8 700 руб., заемщику будет выгоднее точный расчет методом 365/365, по которому он уплатит минимальную сумму процентов 8 580,82 руб.□

Если процентная ставка меняется во времени, то наращенная сумма вычисляется по формуле

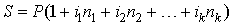где n₁, n₂, …, n_k – интервалы времени, следующие друг за другом; (n₁ + … + n_k = n), i₁, i₂, …, i_k – соответствующие им ставки процентов.

Пример 3.

Контракт предполагает следующий порядок начисления простых процентов: первый год – 16 % годовых, в каждом следующем полугодии ставка повышается на 1 %. Определите множитель наращения за 2,5 года. Оцените, на сколько процентов увеличится сумма контракта за этот срок.

Решение. Срок контракта n = 2,5 года разбит на 4 периода (k = 4):

1) i₁ = 0,16; n₁ = 1;

2) i₂ = 0,17; n₂ = 0,5;

3) i₃ = 0,18; n₃ = 0,5;

4) i₄ = 0,19; n₄ = 0,5.

Находим множитель наращения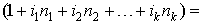

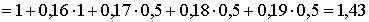– во столько раз увеличится сумма контракта за 2,5 года, что соответствует увеличению на 43 %.

Сумма, полученная в результате начисления простых процентов, может быть вновь инвестирована под ту же или другую процентную ставку. В случае многократного инвестирования (реинвестирования) в пределах расчетного срока n формула наращения имеет вид

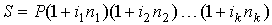где n₁, n₂, …, n_k – длительности последовательных периодов реинвести­рования (n₁ + … + n_k = n), i₁, i₂, …, i_k – ставки реинвестирования.

Пример 4.

На сумму 100 тыс. руб. начисляется 20 % годовых (проценты простые, точные, с точным числом дней). Определите наращенную сумму, если операция реинвестирования проводится ежемесячно в течение первого квартала не високосного года. Сравните результат с наращением без реинвестирования процентов.

Решение. P = 100 000; i = 0,2. Срок операции разбит на 3 расчетных периода (k = 3):

1) январь; n₁ = 31/365;

2) февраль; n₂ = 28/365;

3) март; n₃ = 31/365.

При ежемесячном реинвестировании процентов имеем

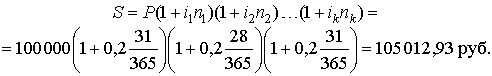Без реинвестирования процентов n = 90/365:

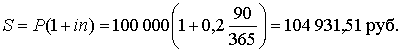Видно, что при реинвестировании процентов наращенная сумма больше.
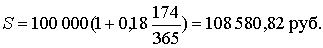