Мы привыкли измерять длину в метрах, вес в килограммах. В компьютере наименьшей единицей информации является бит. Количество информации, содержащейся в m-разрядном сообщении (состоящем из m знаков), когда каждый знак равновероятно взят из N-значного (то есть состоящего из N знаков) алфавита, вычисляется по формуле

I = m×

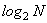которая следует из формулы Хартли. Количество знаков в алфавите называется его мощностью.

Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации, подсчитывается просто по количеству двоичных знаков, которое требуется для такой записи. Чаще всего в качестве наименьшей единицы измерения объема информации используется байт, состоящий из 8 бит (1 б = 8 бит). В каждой ячейке внутренней памяти содержится 1 байт. Байты объединяются в более крупные наборы в зависимости от цели использования (ввод, вывод, передача по каналам связи между устройствами и т.д.).

Для измерения объема памяти используются и более крупные, чем бит или байт, единицы измерения, называемые килобайтом (Кб), мегабайтом (Мб) и гигабайтом (Гб). Переход от меньшей единицы измерения к большей осуществляется с помощью коэффициента 2¹⁰ = 1024. Для измерения памяти большого объема используют единицы измерения терабайт (1 Тб = 1024 ГБ) и петабайт (1 ПБ = 1024 Тб)

Например, в слове информатика 11 знаков. Если это слово составлено с использованием 32-значного алфавита, то имеем N = 32 и m = 11. Тогда количество информации в этом слове равно

I = 11×

= 11×5 = 55 бит

формулы Хартли

Каждый бит может принимать одно из двух значений (0 или 1), поэтому последовательность из I бит может принимать N = 2^I различных значений. Следовательно, для любого N-значного алфавита количество бит, которое требуется для представления любого из этих знаков, вычисляется по формуле

I =

которая называется формулой Хартли. Эта величина принимается в качестве количества информации, содержащейся в сообщении, состоящем из одного знака N-значного алфавита, когда каждый знак может быть равновероятно взят из этого алфавита.

равновероятно

Формула Хартли предполагает, что каждый знак равновероятно берется из алфавита. Если вероятности появления знаков различны, то количество информации, содержащейся в сообщении, состоящем из m знаков, вычисляется по формуле Шеннона

I =

где P_i – вероятность появления i–го знака.

по количеству двоичных знаков

При этом, в частности, невозможно нецелое количество битов (в отличие от количества информации).

байт

Поскольку каждый бит обеспечивает представление одного из двух значений 0 или 1, то каждый байт может принимать 2⁸ = 256 различных значений от 00000000 до 11111111.

с помощью коэффициента

Соответственно, 1 Кб = 1024 б, 1 Мб = 1024 Кб (около одного миллиона байтов), а 1 Гб = 1024 Мб (около одного миллиарда байтов).