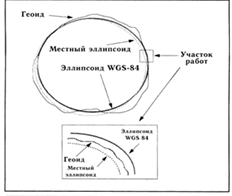
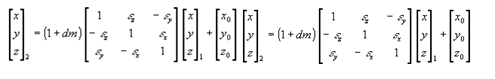Системы координат описывают референцную модель Земли, но этого не достаточно для детального описания требуемой территории. Выбрав систему координат, необходимо решить в каком виде нужно отобразить точку земной поверхности. Наиболее просто отобразить точку в геодезических координатах (широта и долгота). В картографии сферическую поверхность Земли изображают на плоскости. Законы преобразования широты и долготы в плоские координаты Х и Y, называются картографическими проекциями. Математические модели могут быть близки к описываемой поверхности, но не являются её копиями. Однако, для описания локальных областей, в пределах заданной точности, в геодезии применяются простые эллипсоидальные или сферические модели земной поверхности. Такой моделью, например, является эллипсоид вращения. На практике не удаются изобразить поверхность Земли без площадных, линейных и угловых искажений в одной проекции. Один из этих параметров всегда будет искажаться. Нужно выбрать ту проекцию, которая наиболее полно отвечает решаемым задачам. Существует множество местных систем координат, параметры которых заданы на основе известных эллипсоидов и проекций. Например, системы СК-42, СК-63, U.S. State Plane, Australian Map Grid, New Zealand Map Grid, Ordinat Survey of Great Britain и многие другие. При этом используются проекция Гаусса-Крюгера, Поперечная проекция Меркатора, а для Аляски (которая имеет вытянутую, узкую форму) Косоугольная проекция Меркатора. При этом нельзя задать такой эллипсоид, который бы наиболее правильно описывал всю земную поверхность, для описания различных областей используют разные модели эллипсоидов наиболее точно совпадающих с земной поверхностью в данном районе (рис.3.5).

Для представления данных ГИС в местной системе координат, очень важно понимать, что есть большие различия в отображении GPS позиций в системе координат WGS-84, и отображении тех же позиций в местной системе координат на основе местных ИГД. Картографические программные продукты позволяют переводить данные  из системы координат WGS-84 в местные системы координат, а также преобразовывать высоту над эллипсоидом WGS-84 в высоту над геоидом. Программное обеспечение может отображать данные в системе координат заданной пользователем, и преобразовывать их на выходе в формат ASCII или в форматы совместимые с заданной базой данных.

 

 

Рис.3.5. Модели эллипсоидов, описывающих земную поверхность

 

Геодезические системы отсчета (Reference Systems) устанавливают параметры, определяющие фигуру, размеры, гравитационное поле Земли и закрепляют гринвичскую геоцентрическую прямоугольную систему координат. Общепризнанными (международными) системами отсчета являются IERS (International Earth Rotation Service),  ее европейская подсистема ETRS (European Terrestrial Reference System),   система GRS-80 (Geodetic Reference System, 1980), параметры которой служат основой ряда других систем Европы, Австралии и Америки. В настоящее время в связи с широким применением спутниковых систем позиционирования в мире получила распространение геоцентрическая координатная система WGS-84 (World Geodetic System,1984г.,США), в которой заданы орбиты спутников. Начало отсчета системы расположено в центре масс Земли с точностью около 1 м., одна из осей проходит через Северный полюс, вторая – через Гринвичский меридиан.  Ее физические параметры практически соответствуют параметрам эллипсоида GRS-80 (табл3.2). WGS-84 сейчас стала де-факто международной системой навигации. Все аэропорты мира, согласно требованиям ICAO, определяют свои аэронавигационные ориентиры в WGS-84. Россия не является исключением. С 1999 г. издаются распоряжения о ее использовании в системе нашей гражданской авиации (Последние распоряжения Минтранса № НА-165-р от 20.05.02 г. «О выполнении работ по геодезической съемке аэронавигационных ориентиров гражданских аэродромов и воздушных трасс России»)                                                    

В России без интеграции с западными странами создана система координат Параметры Земли 1990 г- ПЗ-90 (табл.3.2). Система ПЗ-90 закреплена координатами трех десятков опорных пунктов Космической геодезической сети России, при этом 7

 

Таблица 3.2. 

Геометрические параметры референц-эллипсоидов

пунктов установлены в Антарктиде. Погрешность взаимного положения пунктов при расстояниях между ними до 10 000 км составляет менее 30 см. Начало координат геоцентрической системы координат ПЗ-90 совмещено с центром масс Земли с точностью около 1 м. ОСЬ Z направлена на Условный полюс Земли, как определено в рекомендации Международной службы вращения Земли (IERS); ОСЬ X направлена в точку пересечения плоскости экватора и нулевого меридиана, определенного Международным бюро времени (BIH); ОСЬ Y дополняет геоцентрическую прямоугольную систему координат до правой. Геодезические координаты точки в системе координат ПЗ-90 относятся к эллипсоиду, значения большой полуоси и полярного сжатия которого даны в таблице 3.2. Геодезическая широта В точки М определяется как угол между нормалью к поверхности эллипсоида и плоскостью экватора. Геодезическая долгота L точки М определяется как угол между плоскостью нулевого меридиана и плоскостью меридиана, проходящего через точку М. Положительное направление счета долгот - от нулевого меридиана к востоку. Геодезическая высота H определяется как расстояние по нормали от поверхности эллипсоида до точки М.

Параметры общеземных систем координат WGS-84 и ПЗ-90 постоянно уточняются. Такие системы удобны для описания положения космических объектов в околоземном пространстве. Однако картографические материалы созданы в различных топоцентрических системах. В них начало отсчета расположено в точке на поверхности Земли (например, на экваторе), одна из осей проходит через полюс, вторая ей перпендикулярна. В России большинство топографических материалов создано в цилиндрической проекции Гаусса – Крюгера. Многие объекты могут обрабатываться и в частных топоцентрических проекциях. Но использовать пространственные геоцентрические координаты для решения прикладных задач картографирования или проектирования нельзя, поскольку в этой системе, например, невозможно определить направление стока воды. В связи с этим возникает задача перевычисления уравненных в общеземной геоцентрической системе координат в требуемую (государственную или частную) топоцентрическую систему.

Преобразование пространственных прямоугольных или эллипсоидальных координат одной координатной системы в другую координатную систему того же типа по достаточно строгим формулам с использованием точно определенных параметров перехода является достаточно простой задачей для трехмерных координатных систем ПЗ-90 и СК-42 и связанных с ними двумерных топоцентрических систем (государственная система координат, местная система координат), а также для трехмерных систем WGS-72 и WGS-84 и связанных с ними двухмерных топоцентрических систем (NAD-87 и др.).  Все сказанное справедливо, кроме случая связи систем координат ПЗ-90 и WGS-84 – базовых для национальных космических навигационных систем ГЛОНАСС и GPS. Взаимосвязь между WGS-84 и ПЗ-90 устанавливают при помощи известных  формул Гельмерта, хотя исследования этой взаимозависимости  продолжаются (табл.3.3.). В настоящее время нужна точная связь между двумя координатными системами, чтобы в полной мере воспользоваться их возможностями.

Таблица 3.3 Параметры Гельмерта перехода между некоторыми системами координат

Система координат	Tx , м	Ty ,м	Tz ,м	m * 10-6	Rx ,угл.сек	Ry ,угл.сек	Rz ,угл.сек
ITRF-93 к WGS-84	0.074	-0.500	-0.238	-0.0105	+0.01869	-0.00110	+0.00796
WGS-84  к CК-42	-25	141	78.5	0	0.35	0.736	0
ПЗ-90 к CК-42 [9]   [Pinacle]	-26.6        -25.0        -26.45	134.8 141.0  131.3	77.3   80.0   74.6	0.06   0.00     0.4	0.17         0.35   0.22	0.39          0.66      0.4	0.83   0.00     0.90
ПЗ-90 к CК-95	-25.9	130.94	81.76	0.00	0.00	0.00	0.00
ПЗ-90 к WGS-84 [9]	-0.3± 0.6	2.2± 0.7	1.0± 0.6	-0.06± 0.09	-0.049± 0.03	-0.01± 0.02	-0.07± 0.02
ПЗ-90 к WGS-84 [6]	0	0	1.5	0	0	0	-0.076
ПЗ-90 к WGS-84 [10]	0	0	4	0	0	0	-0.6

 Помимо международных, существуют национальные системы отсчета, называемые в нашей стране референцными. Центры их эллипсоидов часто не совмещены с центром масс Земли. Они устанавливают квазигеоцентрические координаты. Например, в системе координат 1942 г. на референц-эллипсоиде Красовского (СК-42) центр эллипсоида смещен с центра масс Земли более, чем на 155 м. Положения точки в пространстве, определенные по координатам указанных геоцентрических систем, могут различаться до десятка метров, что создает дополнительные проблемы при организации мониторинга оползневых процессов. Различия же координат геоцентрических и квазигеоцентрических систем значительно больше и могут превысить сотню метров  

 Различия разных общеземных координатных систем обусловлены именно особенностями построения и обработки геодезических сетей. В IERS новейшими методами космической геодезии установлена сеть станций ITRF (IERS Terrestrial Reference Frame). Сети закрепляют начало координат в центре масс Земли с точностью до 10 см, ориентируют ось Z на Условный земной полюс с погрешностью в сотых долях угловой секунды и устанавливают ось X в плоскости меридиана Гринвича до тысячных долей секунды. Со временем геоцентрические координаты пунктов опорных сетей вследствие непрерывного их совершенствования и геодинамических процессов изменяются. Эти изменения могут достигать 1-2 см в год. Поэтому каталоги координат обновляют и указывают их эпоху, например, ITRF-89, ITRF-94 и т.д.
           Спутниковые системы определяют координаты точек в общеземных системах: GPS - в WGS-84, ГЛОНАСС - в ПЗ-90.  Используют же координаты в референцной, например в СК-42, или местной системе. Возникает необходимость пересчета координат из одной системы в другую. Общеземные геоцентрические координаты WGS-84 пересчитывают в геодезические широты B, долготы L и высоты H. Геодезические высоты трансформируют в ортометрические высоты H^g. По геодезическим широтам и долготам вычисляют плоские прямоугольные координаты, например, в проекции UTM. От вычисленных таким образом координат необходимо перейти к соответствующим координатам, применяемым в России. Переход может быть выполнен на любом этапе. Естественно в самом начале перейти от WGS-84 к ПЗ-90, затем на эллипсоид Красовского, вычислить геодезические координаты, нормальные высоты и плоские координаты Гаусса-Крюгера.  

 Но следует иметь в виду, что геодезические широта B, долгота L и высота над эллипсоидом по нормали к нему H даны относительно того эллипсоида, которым пользуется система спутникового позиционирования. Так, в случае GPS они вычисляются для земного эллипсоида WGS-84. Российская государственная система координат - «Система координат 1942 г.», или СК-42, (как и пришедшая ей недавно на смену СК-95) отличается тем, что, во-первых, основана на эллипсоиде Красовского, несколько большем по размерам, чем эллипсоид WGS-84, и во-вторых, Российский  эллипсоид сдвинут (примерно на 150 м) и слегка развернут относительно общеземного. Всё потому, что наша геодезическая сеть покрыла шестую часть суши еще до появления спутников. Эти отличия приводят к погрешности GPS на наших картах порядка 0,2 км. После учета параметров перехода эти погрешности устраняются до навигационной точности, но не для геодезической: точных единых параметров связи координат не существует, и виной тому локальные рассогласования внутри государственной сети. Геодезистам приходится для каждого отдельного района самим искать параметры трансформирования в местную систему.

При решении задач картографии, навигации и др. необходимо использовать координатную поверхность отсчетного эллипсоида и связанные с ней геодезические координаты. В геодезической системе координат положение точки определяется высотой H над принятым референц-эллипсоидом, широтой B и долготой L. Геодезическая широта определяется как угол, образованный нормалью к поверхности эллипсоида с плоскостью его экватора. Геодезическая долгота – двухгранным углом между плоскостями начального меридиана и меридианом данной точки. Преобразование эллипсоидальных геодезических координат в прямоугольные осуществляется по формулам:
X = (N + H) cosB cosL; Y = (N + H) cosB sinL;  Z = (b²/a²N + H) sinB, /

Начало координат X, Y, Z совпадает с центром отсчетного эллипсоида. Эллипсоид ориентирован так, что его малая ось параллельна среднему положению оси вращения Земли, а плоскости начальных астрономического, Гринвичского, и геодезического меридианов параллельны. Геодезические широты B дополняют до 90^° угол между нормалью к эллипсоиду и его малой осью, долготы отсчитываются от начального меридиана. Геодезические широта и долгота исходного пункта астрономо-геодезической сети, находящегося в Пулковской обсерватории, были приравнены к астрономической широте и долготе. Принято, что в этой точке отвес совпадает с нормалью к эллипсоиду и, следовательно, астрономические азимуты равны геодезическим. При установлении системы координат 1942 г. полагали использовать систему ортометрических высот и высот геоида над эллипсоидом. Но поскольку вычисления выполнены по упрощенным формулам, результаты оказались близкими к нормальным высотам и высотам квазигеоида в соответствии с теорией профессора М. С. Молоденского, опубликованной в 1945 г. Закрепление системы координат 1942 г. на поверхности Земли выполнено раздельно астрономо-геодезической сетью пунктов (АГС) и нивелирной сетью государственной высотной основы (ГВО). Высоты квазигеоида определялись по астрономо-геодезическим уклонениям отвеса с использованием местной гравиметрической съемки.

В 1995 г. было завершено совместное уравнивание космической геодезической сети (КГС), астрономо- геодезической сети (АГС) и доплеровской геодезической сети (ДГС). По результатам совместного уравнивания получена новая государственная референцная система координат, которую в настоящее время принято называть системой координат 1995 г. (СК-95). Определены также параметры перехода от системы координат 1995 г. к отечественной общеземной системе координат ПЗ-90 (табл. 3.3). Преобразование координат из одной системы координат в другую осуществляется по формулам: X_P = X_W + DX + w_Y Z_W - wY_W + mX_W;    Y_P = Y_W + DY - w_X Z_W - wX_W + mY_W; Z_P = Z_W + DZ + w_X Y_W - wX_W + mZ_W,  где X_W, Y_W, Z_W - координаты в общеземной системе, X_P, Y_P, Z_P - координаты в референцной системе.  В СК-95 сохранены неизменными координаты начального пункта Пулково, эллипсоида Красовского и проекция Гаусса– Крюгера. В новой системе по отношению к общеземной ПЗ-90 полностью выполнены условия параллельности осей OZ и плоскостей нулевых меридианов, чего нельзя было сделать для системы координат 1942 г. без переуравнивания всей государственной геодезической сети. По сравнению с системой СК-42 в новой системе изменились ее начало и ориентировка осей. Начало новой СК-95 находится на расстоянии около 10 м от начала координат СК-42. Непараллельность осей OZ этих систем характеризуется углами разворота w_X = 0¢¢ и w_Y = -0,351¢¢, которым на полюсе соответствует расстояние 10,5 м. Угол между нулевыми меридианами систем составляет 0,661¢¢, что соответствует расстоянию 20 м на экваторе или 13 м на широте 50^°. В новой системе геодезические координаты B, L и соответствующие им координаты x, y в проекции Гаусса-Крюгера изменились на значения до 30 м. Примерно до долготы оз. Байкал изменения координат составляют менее 15 м, что может быть учтено на топографических картах масштабов 1 : 50 000 — 1 : 1 000 000 постепенно, по мере их обновления. Геодезические координаты углов рамок и координатные линии на старых и новых картах будут одинаковыми. Положения контуров относительно углов рамок и координатных линий изменяются на значения до 30 м. Следовательно, несовмещение контуров на старых и новых картах не превысит 0,5 мм на картах масштабов 1 : 50 000 — 1 : 1 000 000.На картах масштабов 1 : 25 000 и 1 : 10 000, составленных в проекции Гаусса–Крюгера, несовмещение контуров будет больше – 0,3 мм. Планы масштабов 1 : 500 – 1 : 5 000 составляют, как правило, в местных системах плоских прямоугольных координатах x, y. Для местных систем необходимо вычислить новые ключи пересчета координат в системе 1995 г. из проекции Гаусса–Крюгера в проекцию Гаусса с местными координатными сетками при условии минимальных изменений прежних значений координат x, y. Координаты x, y в старых и новых местных системах будут различаться во много раз меньше, чем координаты x, y в проекции Гаусса–Крюгера в старой и новой государственных системах.

Референцные и общеземные системы, используемые в разных странах или отнесенные к разным эпохам, различаются по расположению начал x₀, y₀, z₀, разворотом осей на малые углы , , и разностью масштабов dm. В общем случае связь двух систем  устанавливается формулой [Антонович, 2005],

 

В России и странах СНГ до 1 июля 2002г. будет использоваться референцная система 1942 г., введенная по Постановлению Совета Министров № 760 в 1946г. для выполнения работ на всей территории тогдашнего СССР. С 1 июля 2002г. согласно Постановлению Правительства РФ от 28 июля 2000г. № 568 вводится новая референцная система СК-95 и новая общеземная система ПЗ-90. Первая система используется при выполнении геодезических и картографических работ, вторая - для геодезического обеспечения орбитальных полетов. Численные параметры перехода приводятся в руководствах или сообщаются пользователю в технических заданиях.