1.3. Форма и размеры Земли

Для правильного изображения земной поверхности в виде планов и карт необходимо знать фигуру Земли. На физической поверхности Земли встречаются самые различные неровности: горы, хребты, долины, котловины и т.д. Описать такую фигуру какой-то аналитической зависимостью невозможно. В то же время, для решения многих геодезических задач надо основываться на какой-то математически строгой фигуре, только тогда возможно получение расчётных формул и методов для определения координат и ориентирования на земной поверхности, в том числе для создания карт. Поэтому задачу по определения формы и размеров Земли принято делить на две части:

1)           установить форму и размеры некоторой геометрически правильной фигуры, представляющей Землю в общем виде;

2)           изучить отступления реальной физической поверхности Земли от этой фигуры.

Земля, в первом приближении, может считаться шаром. Но на нее воздействует центробежная и центростремительная силы. В результате, она сжимается с полюсов и растягивается по экватору.

При этом необходимо отметить, что:

• Центробежная сила, как результат вращения вокруг оси, делала бы Землю правильным эллипсоидом вращения, если бы она была изотропна.
• Геологические силы - внутренние (эндогенные) и внешние (экзогенные) - делают внутреннее строение Земли и ее поверхность очень сложным. Все эти силы искажают форму Земли и делают её геоидом. Из-за горообразовательных процессов, движения литосферы и неоднородности строения литосферы, вариаций в плотности разных зон Земли и литосферных пород.

 

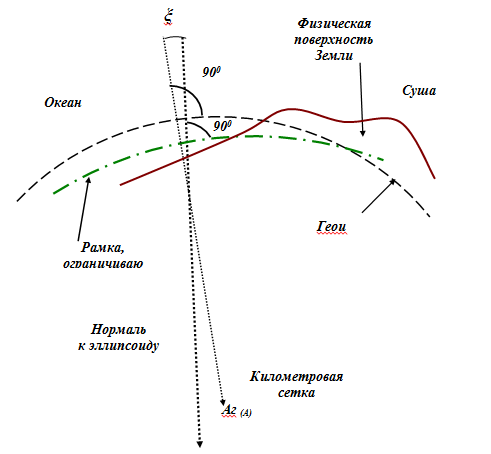
Рис. 1. Форма земли: ξ – угол между отвесной линией и нормалью к эллипсоиду

Известно, что 71 % земной поверхности покрывают моря и океаны, доля суши составляет только 29 %. Поверхность морей и океанов, находящаяся в спокойном состоянии, характерна тем, что она в любой её точке перпендикулярна к отвесной линии, т. е. к направлению действия силы тяжести. Направление действия силы тяжести можно установить в любой точке простым прибором и, соответственно, построить поверхность, перпендикулярную к направлению этой силы. Такая поверхность называется уровенной (рис. 1).

Основная (исходная, ну

левая) поверхность - уровенная поверхность, совпадающая со средним уровнем воды в морях и океанах в их спокойном состоянии и мысленно продолженная под материками.

В геодезии за общую фигуру Земли принимают тело, ограниченное основной уровенной поверхностью, и такое тело именуется «геоид» (рис.1). Тем не менее, поверхность геоида не может служить той формой, относительно которой можно изучать физическую поверхность Земли, так как аналитической зависимостью точно описать геоид невозможно. Это обусловлено тем, что плотности масс, составляющих земную кору, распределены неравномерно. Кроме того, эти массы под действием внешних и внутренних сил перемещаются (в частности, перемещаются и материковые плиты), следовательно, меняется положение отвесных линий и сама форма геоида.

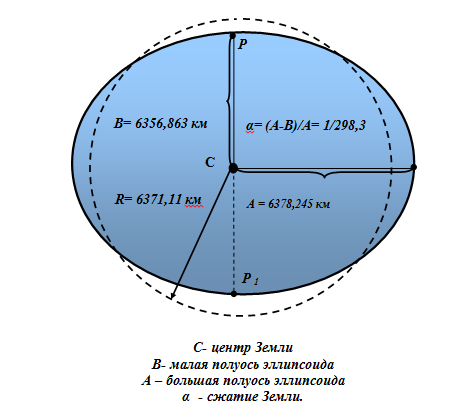
Вследствие особой сложности, то есть  геометрической неправильности геоида, его заменяют другой фигурой – эллипсоидом, который получается при вращении эллипса вокруг его малой оси РР₁ (рис. 2). Размеры эллипсоида определялись учёными ряда стран. В России они были вычислены под руководством профессора Ф. Н. Красовского в 1940 г. и в 1946 г. утверждены постановлением Совета министров.

 

Рис. 2. Эллипсоид вращения

 

Земной эллипсоид ориентируют в теле Земли так, чтобы его поверхность в наибольшей мере соответствовала поверхности геоида. Отклонения геоида от эллипсоида в отдельных местах составляет не более 100-150 м. В тех случаях, когда при решении практических задач фигуру Земли принимают за шар, то радиус шара, равновеликого по объёму эллипсоиду Красовского, составляет:

Такие отступления от действительной фигуры Земли целесообразны, т.к. упрощается проведение геодезических работ. Но эти отступления приводят к искажениям при отображении физической поверхности Земли тем методом, который принят в геодезии – методом проекций.