Пусть потенциальная энергия U(x) частицы зависит только от одной координаты. Для нахождения проекций силы путём дифференцирования по координатам функции потенциальной энергии следует задать явную функциональную зависимость этой величины. Пусть, например, потенциальная энергия зависит от координаты х следующим образом:

$U(x)=6000e^{-\mathrm{0,0005}x}{\sin }^2(\mathrm{0,0015}x)$.

(1)

 

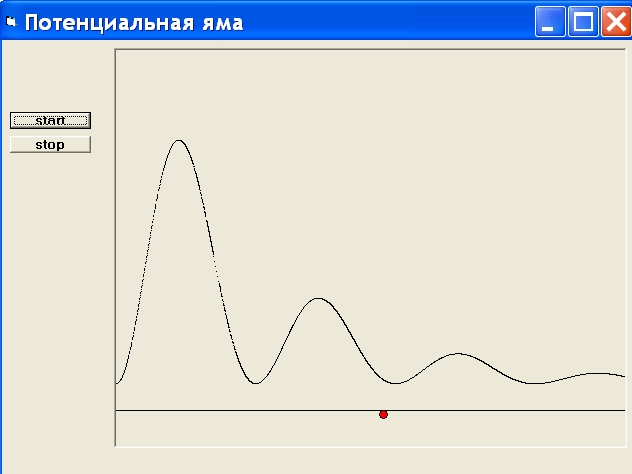
При стремлении х к бесконечности потенциальная энергия обращается в нуль, функция имеет точки максимумов и минимумов. Примерный график зависимости потенциальной энергии от координаты изображён на рисунке ниже.

Необходимо создать программу для определения положения равновесия частицы в этой потенциальной яме. При компьютерном моделировании этой задачи необходимо задать аналитически уравнение потенциальной кривой, так как в этом случае автоматически задаётся также аналитическое выражение для проекции силы на координатную ось.  Дифференцируя (1) по координате, получаем выражение для единственной отличной от нуля проекции силы

$\begin{array}{l}{F}_x=6000[-\mathrm{0,0005}{\sin }^2(\mathrm{0,0015}х)+\mathrm{0,003}\sin (\mathrm{0,0015}x)\times \\ \times \text{сos}(\mathrm{0,0015}x)]e^{-\mathrm{0,0005}x}\end{array}$

(2)

Необходимо предусмотреть возможность изменения начального положения частицы (например, при помощи мышки). У потенциальной кривой имеются точки максимума и минимума, которые соответствуют положениям равновесия. В точке минимума равновесие является устойчивым, а в точке максимума – неустойчивым. Движение частицы в ходе выполнения программы всегда будет происходить в сторону того из устойчивых положений равновесия, которое не отделено потенциальным барьером от заданного начального положения частицы.

При этом глубина минимума безразлична, частица движется как в сторону глубоких, так и в сторону более мелких минимумов. Таким образом, при использовании вариационного метода для молекулярных систем нужно быть осторожным, так как рассматриваемая система может попадать не только в стабильные, но и в метастабильные состояния, отвечающие не самым глубоким минимумам энергии.

Кадр из данного компьютерного эксперимента приведён на рисунке. Соответствующая компьютерная программа дана в приложении.