Наконец, остановимся на разновидности метода Монте-Карло, обычно применяемой в молекулярной физике для конструирования «виртуальных» ансамблей Гиббса и известной как метод Метрополиса [10].

Любое макроскопическое состояние молекулярной системы включает в себя множество микросостояний, в которых молекулярная система находится в разные моменты времени. Для расчёта средних значений физических величин Гиббсом был предложен метод ансамблей. Вместо рассмотрения реальной макроскопической системы в этом методе рассматривается совокупность мысленных копий реальной системы, находящихся в одинаковых внешних условиях, которая называется ансамблем систем.

Разные системы, входящие в ансамбль, находятся в различных микросостояниях, причём некоторые микросостояния встречаются часто, а другие – редко. Вероятность встретить систему в каком-то конкретном микросостоянии зависит от внешних условий, совокупность которых определяет вид ансамбля. В термодинамическом пределе, т.е. при стремлении числа частиц к бесконечности, применение любого ансамбля Гиббса приводит к одинаковым результатам.

Наиболее часто применяется так называемый канонический ансамбль Гиббса, в котором вероятность встретить в ансамбле систему с энергией $U_{i}$ равна:

$w_{i} = \frac{1}{Z} e^{- \frac{U_{i}}{k T}}$ ,

где Z – нормировочный множитель, называемый статистической суммой, Т – абсолютная температура, k – постоянная Больцмана. Среднее значение произвольной физической величины А тогда определяется как математическое ожидание:

$⟨ А ⟩ = \sum_{i} A_{i} w_{i}$ ,

где $A_{i}$ – значение этой величины для i-го микросостояния данной молекулярной системы.

Для реализации метода Метрополиса генерируется случайный марковский процесс, который определяется заданием вероятностей перехода между образующими его состояниями. Для создания «виртуального» ансамбля Гиббса вероятность перехода между состояниями должна быть вполне определённой: например, она пропорциональна больцмановскому множителю $e^{- \frac{Δ U}{k T}}$ для канонического ансамбля и задаётся соответствующими выражениями для других гиббсовских ансамблей. В этой формуле DU – разность энергий всей системы для тех состояний, между которыми осуществляется переход.

Алгоритм метода Метрополиса заключается в следующем. Берётся произвольное начальное состояние изучаемой системы и производится элементарное изменение этого состояния. Например, это элементарное изменение в случае жидкости или газа заключается в смещении на малое расстояние в произвольном направлении одной из частиц, в случае магнетика – в перевороте магнитного момента одного из атомов, для полярного диэлектрика – в повороте дипольного момента одного из атомов на малый угол и т.д. Затем в рамках принятой модели взаимодействия рассчитывается изменение полной энергии всей системы DU при таком элементарном изменении, после чего вычисляется больцмановский фактор $e^{- \frac{Δ U}{k T}}$ . После этого генерируется случайное число р, равномерно распределённое в промежутке от 0 до 1, и сравнивается с больцмановским множителем. Если р < $e^{- \frac{Δ U}{k T}}$ , то данное испытание принимается, новое состояние включается в состав виртуального ансамбля Гиббса и применяется при расчёте средних по ансамблю величин. При обратном неравенстве испытание отвергается и в состав ансамбля ещё раз включается старое состояние, а следующее испытание производится независимым образом. Отметим, что в случае уменьшения энергии системы в результате элементарного испытания (т.е. при ΔU < 0) больцмановский фактор всегда больше единицы, и любое случайное число поэтому всегда меньше его. Таким образом, при ΔU < 0 испытание всегда принимается и вычисления больцмановского фактора не требуется.

Для достаточно точного определения средних значений физических величин необходимо произвести достаточно много испытаний (по крайней мере, несколько сот или даже тысяч в расчёте на одну частицу). Если система первоначально не находилась в состоянии термодинамического равновесия, то с течением времени по мере проведения этих случайных испытаний она постепенно приближается к этому состоянию, а затем наблюдаются флуктуации виртуальной системы вблизи него. Время прихода виртуальной системы в состояние равновесия сильно зависит от начального состояния системы.

В качестве примера рассмотрим равновесное распределение частиц идеального газа в однородном поле тяжести. В этом случае каждая молекула обладает потенциальной энергией только во внешнем поле тяжести

U = mgh,а энергия взаимодействия молекул друг с другом не учитывается. Это позволяет очень сильно упростить алгоритм данной задачи, так как основная сложность метода Метрополиса обычно заключается в расчёте изменения энергии взаимодействия при переходе из данного состояния в другое, близкое ему состояние. В данной задаче элементарный шаг заключается в изменении высоты какой-либо частицы на небольшую случайную величину, которая может быть задана как

Δh = C*(RND –0,5),

т.е. может изменяться от –0,5 С до +0,5 С. Здесь RND – случайное число (язык Visual Basic), а С – численный параметр, задаваемый таким образом, чтобы, с одной стороны, шаг был не слишком большим и картина распределения частиц по высоте не выходила бы за пределы экрана, а с другой – он не был бы слишком малым, чтобы равновесное распределение частиц по высоте не устанавливалось бы слишком долго. Изменение энергии всего газа при одном таком элементарном шаге равно изменению потенциальной энергии одной частицы ΔU = mgΔh = mgC(RND –0,5), именно эта величина будет фигурировать в формуле метода Метрополиса.

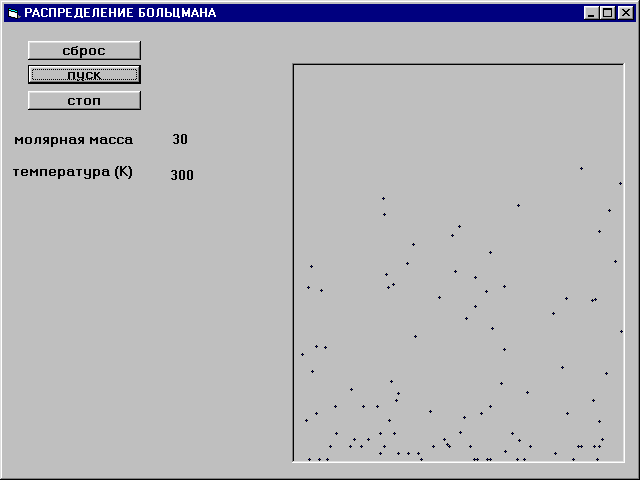
«Опыт» можно провести для разных значений массы частиц m, ускорения свободного падения g и температуры T. Можно продемонстрировать, что при больших значениях m и низких температурах частицы «поджимаются» книзу, а в противоположном случае распределение частиц по высоте становится более равномерным. Кадр из эксперимента приведён на рисунке. Соответствующая компьютерная программа приведена в приложении.