Особое место в применении различных вариантов метода Монте-Карло занимают случаи, когда этот метод используется для организации эволюции изучаемой системы, т.е. как главное средство при создании «виртуального» эксперимента, моделирующего реальную систему.

Рассмотрим в этом параграфе случайное блуждание частицы в плоскости, которое будет имитировать хаотическое движение броуновских частиц. Они представляют собой мелкие (десятые доли микрона) макроскопические частицы. При наблюдении в микроскоп видно, что эти частицы находятся в непрерывном хаотическом движении, похожем на дрожание, которое никогда не прекращается. Это движение открыто в 1827 году английским ботаником Р. Броуном, изучавшим под микроскопом взвесь цветочной пыльцы в воде. Сначала исследователи предполагали, что таким свойством обладает только живая материя, но немного позднее подобное хаотическое движение было открыто и у небольших частиц неорганического происхождения.

Молекулярная теория объясняет броуновское движение нерегулярными соударениями хаотически движущихся молекул с броуновской частицей, нерегулярность этих соударений проявляется вследствие сравнительно малого размера частицы. При этом коллектив броуновских частиц находится в состоянии термодинамического равновесия с молекулярной системой: броуновские частицы имеют такую же среднюю энергию $\frac{3}{2}kT$, как и молекулы, их скорости распределены в соответствии с распределением Максвелла. Во внешних полях броуновские частицы ведут себя подобно идеальному газу, так как их взаимодействием друг с другом из-за больших расстояний между ними можно пренебречь, даже если они помещены в жидкость, поэтому они распределены в пространстве в соответствии с распределением Больцмана, справедливого для классического равновесного идеального газа. 

В простейшей модели броуновское движение можно представить как случайное блуждание частицы (если необходимо наглядное представление, то на плоскости) с переменным или даже с постоянным небольшим шагом. При этом приращения координат х и у на каждом шаге вычисляются независимо друг от друга как случайные величины, принимающие значения от –h до + h, где h – максимальное значение элементарного шага, составляющее небольшую долю размера экрана. Тогда приращение координат определяется выражением

Δх = 2 * h * (RND – 0.5),

Δу = 2 * h * (RND – 0.5),

где случайное число, генерируемое при обращении к функции RND (так эта функция называется на языке Basic или Visual Basic), принимает с равной вероятностью значения от 0 до 1, причём при каждом новом обращении его значение отличается от предыдущего. После определения новых координат частица перерисовывается уже в этом новом положении, в результате она совершает на экране случайное движение, а если имеется коллектив таких частиц, то каждая из них независимо от других будет двигаться по своей случайной траектории.

Для изучения случайных блужданий в начале ХХ века получена формула Эйнштейна – Смолуховского, справедливая для средних значений при большом числе испытаний (или для большого коллектива частиц):

$⟨r^2⟩=\frac{6kT}{b}t$,

где (r²) – среднее значение квадрата расстояния от начального положения броуновской частицы до её положения через промежуток времени t, k – постоянная Больцмана, T – абсолютная температура, b – коэффициент вязкого трения, т.е. коэффициент пропорциональности между силой вязкого трения и скоростью частицы, зависящий от её размеров и вязкости среды, в которой она движется.

Соотношение Эйнштейна – Смолуховского, т.е. прямо пропорциональную зависимость между (r²) и t, легко проверить экспериментально при помощи предлагаемой компьютерной модели. Для этого следует выпускать частицы по одной из какой-то фиксированной точки – начала координат – и определять их положение на экране монитора через одинаковый промежуток времени (можно применять компьютерный таймер или даже ручной секундомер). После нескольких (не менее 20–30) испытаний следует усреднить квадрат расстояния, на которое удалилась частица от начальной точки в течение заданного промежутка времени. Проведя затем подобные серии испытаний для других промежутков времени, можно убедиться в прямо пропорциональной зависимости среднего квадрата расстояния от времени.

Именно таким образом в реальных опытах с броуновскими частицами Ж. Перрен в 1908–1910 годах определил постоянную Больцмана (а из неё число молекул в одном моле – число Авогадро). Исторически этот опыт стал одним из решающих экспериментов при возникновении и становлении молекулярной теории строения вещества, и только после опытов Перрена большинство исследователей – физиков и химиков – признали существование молекул как реальных объектов.

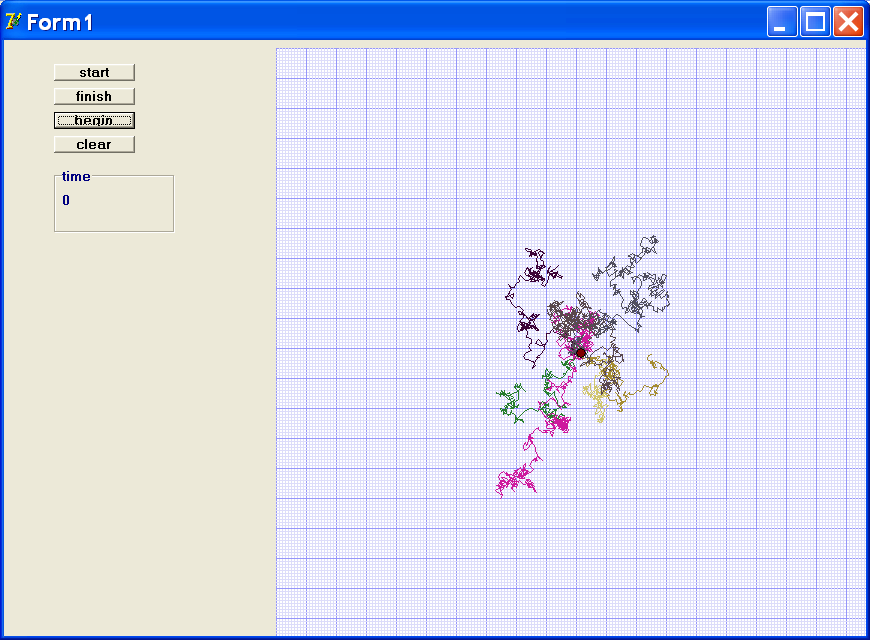
Кадр из компьютерного эксперимента приведён на рисунке. Хаотические траектории броуновских частиц вырисовываются на экране малыми отрезками прямых линий. Соответствующая компьютерная программа на языке Delphi приведена в приложении.