Рассмотрим две материальные точки, взаимодействующие только друг с другом. По 3-му закону Ньютона сила, с которой 1-е тело действует на второе, равна по величине и противоположно направлена по отношению к силе, которая действует со стороны первого тела на второе, причём эти силы действуют вдоль линии, соединяющей материальные точки. Тогда 2-й закон Ньютона для этих тел запишется в виде:

$\begin{array}{l} m_{1} \frac{Δ {\vec{v}}_{1}}{Δ t} = {\vec{F}}_{1,2} \\ m_{2} \frac{Δ {\vec{v}}_{2}}{Δ t} = {\vec{F}}_{2,1} \end{array}$ ,

где $Δ {\vec{v}}_{1}$ и $Δ {\vec{v}}_{2}$ – приращение скоростей 1-го и 2-го тел за время $Δ t$ , а ${\vec{F}}_{1,2}$ и ${\vec{F}}_{\begin{array}{l} 2,1 \end{array}}$ – соответственно сила, действующая со стороны второго тела на первое и наоборот.

Сложим эти уравнения. Сумма правых частей равна нулю, так как вследствие 3-го закона Ньютона ${\vec{F}}_{1,2} = - {\vec{F}}_{2.1}$ . Значит, равна нулю также сумма левых частей уравнений. Таким образом,

$m_{1} Δ {\vec{v}}_{1} + m_{2} Δ {\vec{v}}_{2} = m_{1} ({\vec{v}}_{1}^{″} - {\vec{v}}_{1}^{'}) + m_{2} ({\vec{v}}_{2}^{″} - {\vec{v}}_{2}^{'}) = 0$ ,

где ${\vec{v}}_{1}^{'}, {\vec{v}}_{2}^{'}$ – скорости 1-го и 2-го тел в начале промежутка времени $Δ t$ , а ${\vec{v}}_{1}^{″}, {\vec{v}}_{2}^{″}$ – в конце этого промежутка. Из этого уравнения получаем:

m_{1} {\vec{v}}_{1}^{″} + m_{2} {\vec{v}}_{2}^{″} = m_{1} {\vec{v}}_{1}^{'} + m_{2} {\vec{v}}_{2}^{'}

(1)

Величина, равная произведению массы материальной точки на её скорость, называется импульсом. Для системы материальных точек полный импульс равен сумме импульсов. При этом следует иметь в виду, что импульс – это векторная величина, и поэтому в общем случае импульсы складываются как векторы, т.е. по правилу параллелограмма. Уравнение (1) выражает закон сохранения импульса для двух материальных точек, которые взаимодействуют только между собой. В правой и левой частях уравнения стоит суммарный импульс двух тел в разные моменты времени, из уравнения видно, что эта величина остаётся неизменной (т.е. сохраняется).

Таким образом, закон сохранения импульса можно сформулировать так: если на тела системы действуют только силы взаимодействия между ними («внутренние силы»), то полный импульс системы тел не изменяется со временем, т.е. сохраняется. Этот закон применим не только к системе двух тел, как в рассмотренном примере, но и к системе, состоящей из любого числа тел.

Закон сохранения импульса выполняется при распаде тела на части и при абсолютно неупругом ударе, когда соударяющиеся тела соединяются в одно. Если распад или удар происходят в течение малого промежутка времени, то закон сохранения импульса приближённо выполняется для этих процессов даже при наличии внешних сил, так как за малое время внешние силы не успевают значительно изменить импульс системы. Если внешние силы имеют какое-то определённое направление, то сохраняется не сам импульс, а его проекции на оси, перпендикулярные действующей силе.

Рассмотрим движение тела, брошенного под углом к горизонту. Пусть тело бросили со скоростью $v_{0}$ под углом $α$ к горизонту (рис. 1). В полёте на тело действует сила тяжести, направленная вниз, поэтому горизонтальная проекция скорости не изменяется со временем и равна $v_{x} = v_{0} \cos α$ .

Пусть в верхней точке траектории тело распадается на 2 одинаковых осколка, причём скорость одного из осколков, равная v, задаётся. При распаде выполняется закон сохранения горизонтальной проекции импульса, поскольку сила тяжести направлена вертикально. Закон сохранения проекции импульса тогда запишется следующим образом:

$m v_{x} = \frac{1}{2} m v + \frac{1}{2} m v^{'}$ ,

где $v^{'}$ – скорость второго осколка после распада. Из этого равенства получаем:

$v^{'} = 2 v_{х} - v$ .

Поскольку оба осколка сразу же после распада имеют только горизонтальные проекции скорости и находятся на одинаковой высоте, то время их падения также одинаково, т.е. горизонтальные дальности их полёта после распада связаны таким же соотношением, что и скорости, т.е.

$S^{'} = 2 S - s$ ,

где $S$ – горизонтальная дальность полёта от точки бросания до точки разрыва, а s – дальность полёта полетевшего вперёд осколка, имеющего заданную скорость. Расстояние $S^{'}$

считается положительным, если второй осколок полетел вперёд и отрицательным в противном случае.

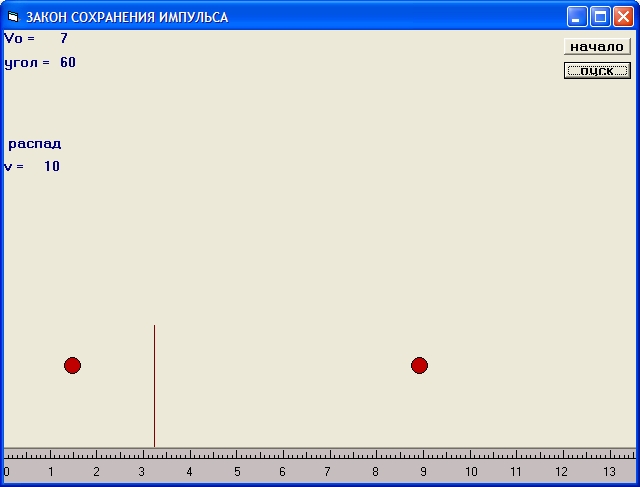
Рис. 2

На рис. 2 изображён кадр из данного компьютерного эксперимента. Дальность полёта осколков тела после распада определяется по линейке. Из точки распада опускается вниз вертикальная линия красного цвета, чтобы отметить эту точку. Измеряя эти расстояния по горизонтальной линейке, можно судить о выполнении закона сохранения импульса. Программа данного компьютерного эксперимента находится в приложении.