Ангармонические колебания играют в природе существенную роль, определяя такие явления как тепловое расширение и деформации твёрдых тел, сегнетоэлектричество и т.д. В то же время в курсах общей физики и классической механики детальное рассмотрение проводится обычно лишь для гармонических колебаний, ангармонические колебания почти не изучаются ни в теории, ни на практике. В данном параграфе описывается компьютерный эксперимент, посвящённый изучению механических ангармонических колебаний, положение равновесия у которых зависит от параметров системы.

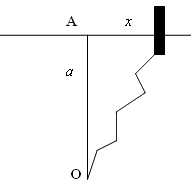Виртуальная “установка” представляет собой небольшую муфточку, которая может скользить без трения по длинному стержню, причём муфточка соединена упругой пружиной с неподвижным упором О. Пусть длина пружины в недеформированном состоянии l₀, расстояние от точки закрепления пружины О до точки А равно а, а расстояние от муфточки до точки А равно х. Потенциальная энергия деформированной упругой пружины равна $U = k {(\sqrt{a^{2} + x^{2}} - l_{0})}^{2} / 2$ . Разложим это выражение в степенной ряд по величине х вблизи точки А (около значения х = 0):

$U = U_{0} + A x + B x^{2} + C x^{3} + D x^{4} + ...$ ,

где коэффициенты разложения имеют следующий вид:

$U_{0} = k {(a - l_{0})}^{2} / 2$ ,

$A = 0$

$B = \frac{1}{2} k (1 - l_{0} / a)$

$C = 0$

$D = k \frac{l_{0}}{8 a^{3}}$ .

Линейный член разложения А равен нулю, т.е. в точке х = 0 всегда находится положение равновесия, соответствующее экстремуму потенциальной энергии.

В случае l₀ < a, который соответствует перерастянутой пружине, коэффициент В > 0, т.е. данный экстремум тогда является минимумом, а окрестность вблизи него представляет собой локальную потенциальную яму (устойчивое положение равновесия), в которой частица может совершать колебания, при малых амплитудах являющиеся гармоническими.

При l₀> a коэффициент В отрицателен, и положение равновесия х = 0 теперь является неустойчивым, а область вблизи него представляет собой потенциальный барьер. По обе стороны этого барьера находятся 2 симметрично расположенные потенциальные ямы, соответствующие устойчивому положению равновесия частицы.

Приравнивая первую производную U к нулю, найдём, что координаты этих двух точек экстремума

$x_{0} = \pm \sqrt{l_{0}^{2} - a^{2}}$ .

(1)

Вторая производная потенциальной энергии в этих точках положительна, т.е. для пересжатой пружины устойчивое положение равновесия смещается из симметричной точки х = 0, а это старое положение равновесия становится неустойчивым.

Особый интерес представляет случай l₀ = a. При этом условии линейный, квадратичный и кубичный члены разложения равны нулю, и первое отличное от нуля слагаемое пропорционально четвёртой степени х. Таким образом, потенциальная яма в этом случае сильно отличается от параболической, поэтому даже колебания с малыми амплитудами являются ангармоническими. В предельном случае при стремлении к нулю амплитуды колебаний их частота w → 0, т.е. период колебаний становится бесконечно большим. При дальнейшем уменьшении расстояния a происходит статическое смещение положения равновесия в точку с координатой, определяемой формулой (1).

Данная задача представляет интерес в физике твёрдого тела, так как подобное явление наблюдается в случае некоторых фазовых переходов, например при переходе сегнетоэлектрик – параэлектрик в титанате бария и других подобных ионных кристаллах. При определённой температуре (точка Нееля) частота одной из оптических мод колебаний решётки становится равной нулю. В дальнейшем при незначительном изменении температуры изменяется энергия взаимодействия атомов и происходит статическое смещение подрешёток относительно друг друга с образованием новых положений равновесия для ионов решётки и появлением по этой причине спонтанной поляризации ионного кристалла. Этот фазовый переход сопровождается понижением симметрии, его часто называют фазовым переходом типа мягкой моды. Как правило, такое превращение является переходом второго рода.

Для создания такого компьютерного эксперимента применяется динамический метод моделирования. Движение является одномерным, поэтому нужно определить проекцию действующей на тело силы упругости деформированной пружины, которая зависит от текущей координаты движущегося тела. В задаче следует предусмотреть как случай перерастянутой, так и пересжатой пружины. Начальное положение осциллятора следует задавать произвольным, например перемещая его в нужную точку при помощи мышки. Отметим, что в данном компьютерном эксперименте полная механическая энергия осциллятора, состоящая из его кинетической энергии и потенциальной энергии деформированной пружины, должна сохраняться в процессе его движения. Это позволяет применить ещё один приём для повышения устойчивости движения: в начале “опыта” определить полную энергию осциллятора и затем контролировать, чтобы её значение было постоянным на каждом временном шаге, увеличивая или уменьшая рассчитанную скорость в зависимости от того, уменьшилась или увеличилась полная энергия при выполнении данного шага. Кадр из данного компьютерного эксперимента приведён на рисунке ниже, а компьютерная программа – в приложении.