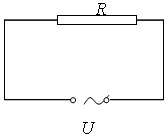
Поместим в цепь переменного тока резистор с сопротивлением R (рис. 1) и подадим на его концы переменное напряжение $U=U_0\cos \text{ω}t$, где ω – циклическая частота колебаний. По закону Ома ток в цепи равен

$I=\frac{U}{R}=\frac{U_0}{R}\cos \text{ω}t=I_0\cos \text{ω}t$,

(1)

Рис.1

где $I_0=\frac{U_0}{R}$ – амплитуда тока.

Отсюда видно, что сдвига фаз между током I и напряжением U нет.

Подключим теперь к цепи переменного тока конденсатор ёмкости С (рис. 2) и подадим на него то же переменное напряжение. Тогда заряд на обкладке конденсатора равен $q=CU=C{U}_0\cos \text{ω}t$. Сила тока в цепи равна

$$$I=\frac{dq}{dt}=-(C{U}_0\text{ω})\sin \text{ω}t=I_0\cos (\text{ω}t+\text{π}/2)$,

(2)

$$где $I_0=C\text{ω}{U}_0=\frac{U_0}{X_C}$.

(3)

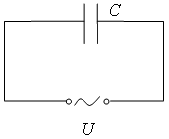Рис.2

Таким образом, в этом случае ток на данном участке цепи изменяется по гармоническому закону с той же частотой, что и подаваемое напряжение, но опережает его по фазе на $\text{π}/\text{2}$. Величина $X_C=\frac{1}{\text{ω}C}$ имеет размерность сопротивления, и в формуле (3), связывающей амплитуды тока и напряжения, она играет как раз эту роль. Эта величина называется емкостным сопротивлением. В предельном случае нулевой частоты она стремится к бесконечности, это означает, что в цепи постоянного тока конденсатор является разрывом в цепи, и ток через него не протекает. При увеличении частоты переменного напряжения емкостное напряжение уменьшается, а для очень высоких частот оно становится ничтожно малым. Это означает, что при больших частотах ток через конденсатор может достигать больших величин. Конечно, электроны движутся только по подводящим к обкладкам конденсатора проводам, между обкладками никакого движения зарядов нет. Однако между обкладками конденсатора имеется быстропеременное электрическое поле, т.е. ток смещения, равный току проводимости в подводящих проводах.

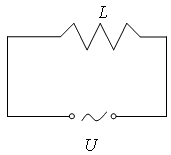
Рис.3

Теперь подключим катушку с индуктивностью L и пренебрежимо малым сопротивлением к цепи переменного тока с синусоидальным напряжением $U=U_0\cos \text{ω}t$ (рис. 3). Запишем закон Ома для участка цепи с э.д.с. $IR=U+\text{ε}$. В нашем случае $R=0$, а $\text{ε}$ – это э.д.с. самоиндукции $\text{ε}=-L\frac{dI}{dt}$. Таким образом $U=L\frac{dI}{dt}$, т.е. $\frac{dI}{dt}=\frac{U}{L}=\frac{U_0\cos \text{ω}t}{L}$. Интегрируя это соотношение, получаем

$$$I=\frac{U_0}{\text{ω}L}\sin \text{ω}t=I_0\cos (\text{ω}t-\text{π}/2)$,

(4)

$$где $I_0=\frac{U_0}{\text{ω}L}=\frac{U_0}{X_L}$.

(5)

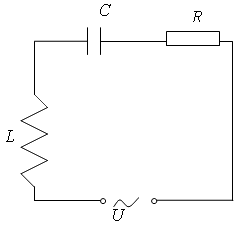Рис. 4

Рис. 5

Из формулы (4) видно, что в этом случае ток изменяется по гармоническому закону с той же частотой, что и подаваемое напряжение, однако отстаёт от него по фазе на $\text{π}/2$. Величина $X_L$, имеющая размерность сопротивления, называется индуктивным сопротивлением катушки. Из формулы (5) видно, что при больших частотах индуктивное сопротивление велико, следовательно, амплитуда тока мала. В случае постоянного тока индуктивное сопротивление, напротив, равно нулю.

Рассмотрим теперь цепочку, состоящую из последовательно соединённых омического сопротивления R, катушки индуктивности L и конденсатора ёмкости С (рис. 4), подсоединенную к источнику переменного напряжения $U=U_0\cos \text{ω}t$. В этом контуре пусть протекает переменный синусоидальный ток силой $I=I_0\cos (\text{ω}t+\text{φ})$. Таким образом мы сделали совершенно естественное предположение о том, что частота изменения тока такая же, как и частота изменения напряжения, но фазы тока и напряжения не совпадают.

Для нахождения амплитуды и начальной фазы тока применим векторную диаграмму (рис. 5). Диаграмма строится следующим образом. Поскольку ток через все элементы контура одинаков, то выберем горизонтальную ось – ось токов. Ток отложим вдоль этой оси в виде вектора, длина которого равна амплитуде тока $I_0$. Вдоль этой оси отложим также напряжение на резисторе, которое изменяется в той же фазе, что и ток. Оно изобразится вектором, длина которого равна $U_R=I_{0}R$.

Векторы, изображающие напряжение на катушке и на конденсаторе, также имеют длину, равную их амплитуде, U_L и U_C соответственно, однако они повернуты на угол $\frac{\text{π}}{\text{2}}$ относительно оси токов: один по часовой, другой против часовой стрелки. Это связано с тем, что при построении векторной диаграммы поворот против часовой стрелки соответствует опережению по фазе, а по часовой стрелке – отставанию.

Вектор, изображающий амплитуду результирующего напряжения U₀  на всей цепочке, будет равен векторной сумме векторов U_R, U_L и U_C. Из рисунка видно, что по теореме Пифагора $U_0=\sqrt{{\left(U_L-U_C\right)}^2+U_R^2}$. Подставляя сюда U_R, U_L и U_C из формул (1), (3) и (5) (там все они обозначены как U₀), получаем

$$$I_0=\frac{U_0}{\sqrt{{\left(X_L-X_C\right)}^2+R^2}}=\frac{U_0}{\sqrt{R^2+{\left(\text{ω}L-\frac{1}{\text{ω}C}\right)}^2}}$.

(6)

Величина омического сопротивлении R называется активным сопротивлением цепи, величина $X=\left|X_L-X_C\right|=\left|\text{ω}L-\frac{1}{\text{ω}C}\right|$ называется реактивным сопротивлением цепи, а

$$$Z=\sqrt{R^2+\left(\text{ω}L-\frac{1}{\text{ω}C}\right)}$  -

(7)

$$

полным сопротивлением или импедансом цепи. 

Различие между активным и реактивным сопротивлением заключается в следующем. При протекании переменного тока через резистор (активное сопротивление) на нем выделяется тепло, которое по закону Джоуля–Ленца равно$Q=I^{2}Rt$. При протекании переменного тока через катушку L и конденсатор C тепло не выделяется. Эти сопротивления называют реактивными.

Из рис. 5 можно определить сдвиг фаз между током и напряжением. На векторной диаграмме он равен углу между амплитудными векторами тока и напряжения, т.е. углу φ. При этом для частного случая, изображённого на рисунке, ток отстаёт от напряжения на величину φ, так как вектор, соответствующий току, повёрнут относительно вектора, соответствующего напряжению, по часовой стрелке. Поэтому, если напряжение изменяется со временем по закону

$$$U=U_0\cos \text{ω}t$,

(8)

$$

то ток – по закону

$$$I=I_0\cos (\text{ω}t-\text{φ})$.

(9)

$$

Из рис. 5 видно, что

$$$\text{tgφ}=\frac{X_L-X_C}{R}=\frac{\text{ω}L-\frac{1}{\text{ω}C}}{R}$,

(10)

причём в нашем частном случае он положителен.

Рис. 6

Построим график зависимости амплитуды тока от частоты подаваемого напряжения, т.е. график функции (6), для разных значений активного сопротивления. Этот график изображён на рис. 6, верхняя кривая соответствует маленькому сопротивлению, нижняя –большому. Из формулы (6) видно, что при частоте, равной нулю, равна нулю также амплитуда тока. В асимптотическом случае при стремлении частоты ω к бесконечности амплитуда тока также стремится к нулю.

Функция имеет единственный максимум, соответствующий минимальному значению знаменателя дроби, при равенстве нулю реактивного сопротивления $X=\left|X_L-X_C\right|=\left|\text{ω}L-\frac{1}{\text{ω}C}\right|$. Отсюда следует, что максимальная амплитуда тока наблюдается при частоте, равной ${\text{ω}}_0=\frac{1}{\sqrt{LC}}$, т.е. при частоте свободных незатухающих колебаний колебательного контура с индуктивностью L и ёмкостью С. Возрастание амплитуды тока при частоте ω₀ является типичным резонансным явлением, а частота ${\text{ω}}_0=\frac{1}{\sqrt{LC}}$

 – резонансной частотой.

Электрический резонанс, наблюдаемый при последовательном соединении активного сопротивления, индуктивности и ёмкости, называется резонансом напряжений. Согласно (10) при резонансе разность фаз между током и напряжением равна нулю, т.е. ток и напряжение совершают колебания в одинаковой фазе. Полное сопротивление цепи при резонансе равно своему наименьшему возможному значению – активному сопротивлению.

Вычислим тепловую мощность, выделяемую в цепи переменного тока. За малое время dt электрические силы в цепи совершают работу $dA=Udq=UIdt$, где dq – протекающий за это время заряд. Подставляя сюда ток и напряжение из формул (8) и (9), получаем $dA=U_0{I}_0\cos \text{ω}t\cos (\text{ω}t-\text{φ})$. Интегрируем это соотношение по времени за один период от нуля до $T=\frac{2\text{π}}{\text{ω}}$, при этом пользуемся тригонометрическим соотношением $\cos \text{α}\cos \text{β}=\frac{1}{2}\left(\cos (\text{α-β})+\cos (\text{α+β})\right)$. Таким образом, полная работа электрических сил за один период равна $A=\frac{1}{2}{U}_0{I}_0{\displaystyle \underset{0}{\overset{T}{\int }}\left(\cos \text{φ}+\cos (2\omega t-\text{φ})\right)}dt=\frac{U_0{I}_{0}T\cos \text{φ}}{2}$, а второй интеграл равен нулю. Таким образом, средняя мощность электрических сил за период равна

$$$N=\frac{A}{T}=\frac{1}{2}{U}_0{I}_0\cos \text{φ}$.

(11)

Эта мощность выделяется на активном сопротивлении в виде тепла, константа cosφ в электротехнике обычно называется коэффициентом передачи мощности. При резонансе в цепи сдвиг фаз между током и напряжением равен нулю, следовательно, коэффициент передачи мощности равен единице. Таким образом, в случае резонанса средняя тепловая мощность                                       

                 $N=\frac{1}{2}{I}_0^{2}R=\frac{U_0^2}{2R}$.

Эта формула напоминает обычный закон Джоуля – Ленца для постоянного тока, отличие только в двойке в знаменателе. Чтобы избавиться от этой двойки и пользоваться привычной формулой Джоуля – Ленца, вводят эффективные или действующие значения силы тока и напряжения, отличающиеся от амплитудных значений этих величин в $\sqrt{2}$ раз: $U_{\text{эф}}=\frac{U_0}{\sqrt{2}}$, $I_{\text{эф}}=\frac{I_0}{\sqrt{2}}$. Именно эффективные значения величин измеряют универсальные электроизмерительные приборы, которыми можно пользоваться как в цепях постоянного, так и переменного тока.

Кадр из компьютерного эксперимента приведён на рис. 7. В правом верхнем углу находится поле, на котором помещаются осциллограммы напряжения (синий цвет) и тока (красный цвет). Амплитуда тока рассчитывается по формуле (6). На осциллограмме её можно измерить при помощи линейки, которая перемещается по рабочему полю в горизонтальном направлении при помощи мышки. Сдвиг фаз между током и напряжением вычисляется по формуле (10), на осциллограмме её можно оценить визуально по горизонтальному смещению относительно друг друга синусоид тока и напряжения. В частности, на рис. 7 сдвиг фаз – около 60 градусов, а амплитуда тока около 12 единиц.

В верхнем левом углу рисуется схема соответствующей электрической цепи, вид которой выбирается при помощи четырёх радиокнопок на поле под осциллограммами. В нижнем левом углу помещаются три радиокнопки для задания периода колебаний подаваемого в цепь напряжения.

Распечатка программы данного компьютерного эксперимента приведена в приложении.

Рис. 7