Основной закон электростатики – закон Кулона – выглядит следующим образом: два неподвижных точечных заряда в вакууме действуют друг на друга с силой, пропорциональной произведению зарядов и обратно пропорциональной квадрату расстояния между ними:

$F = k \frac{q_{1} q_{2}}{r^{2}}$ ,

(1)

где k –коэффициент пропорциональности, зависящий от выбора системы единиц.

Для описания действия заряженных тел друг на друга вводят понятие электрического поля как среды–переносчика взаимодействия. Впервые понятие поля ввел М. Фарадей. Идея заключается в том, что каждое тело создает вокруг себя возмущение окружающего его пространства (поле), которое и действует на другое тело. В качестве индикатора наличия поля можно взять точечный заряд и судить о величине поля в какой-то точке пространства по величине силы, действующей со стороны поля на этот заряд (этот заряд называется пробным). Однако сила зависит и от самого пробного заряда, она пропорциональна его величине. В качестве силовой характеристики вводят напряженность поля - силу, действующую со стороны поля на помещенный в него единичный положительный точечный пробный заряд, т.е. $\vec{E} = \frac{\vec{F}}{q}$ .

Если электрическое поле создано одним точечным зарядом Q, то согласно закону Кулона величина напряженности этого поля равна $E = k \frac{Q}{r^{2}}$ . Если электрическое поле создано совокупностью точечных зарядов, то напряженность результирующего поля равна векторной сумме напряженности полей, созданных каждым точечным зарядом по отдельности. Это утверждение называют принципом суперпозиции, оно равносильно утверждению о том, что множество действующих на тело сил можно заменить их равнодействующей.

Для графического изображения полей вводят силовые линии. Эти линии проводятся так, чтобы, во-первых, в каждой точке напряженность поля являлась касательной к силовой линии, и, во-вторых, силовые линии проводятся гуще там, где больше напряженность поля. Силовые линии электростатического поля не могут пересекаться, они начинаются на положительных и кончаются на отрицательных зарядах или уходят на бесконечность.

Рис. 1

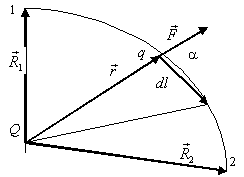
Пусть электрическое поле создано неподвижным точечным зарядом Q, расположенным в начале координат (рис. 1). Будем медленно перемещать в этом поле другой точечный заряд q. При этом на него действует со стороны заряда Q сила $\vec{F}$ , направленная вдоль той же линии, что и радиус-вектор $\vec{r}$ . Вычислим работу, совершенную силами поля при перемещении заряда (другие силы при этом, конечно, тоже могут действовать, но работа этих сил нас не интересует).

Элементарная работа на малом участке $d A = F d l \cos α = k \frac{Q q}{r_{}^{2}} d l \cos α,$ где a – угол между силой и направлением перемещения. Из рисунка видно, что $d l \cos α = d r$ , где dr – приращение модуля радиуса-вектора. Таким образом, $d A = k \frac{Q q d r_{}}{r^{2}}$ . Полная работа, совершенная силами поля при перемещении заряда из начальной точки 1 в конечную точку 2, равна:

$A_{12} = \int_{R_{1}}^{R_{2}} d A = k Q q \int_{R_{1}}^{R_{2}} \frac{d r}{r^{2}} = \frac{k Q q}{R_{1}} - \frac{k Q q}{R_{2}}$ ,

где R₁и R₂– начальное и конечное расстояния между зарядами Q и q. Из этой формулы видно, что работа не зависит от пути, по которому перемещали заряд q, а зависит только от положения начальной и конечной точек.

Для частицы в электростатическом поле можно ввести потенциальную энергию по правилу:

А₁₂ = U₁ – U₂,

(2)

где U₁ и U₂– потенциальная энергия взаимодействия зарядов друг с другом при начальном и конечном взаимном расположении зарядов. Таким образом, потенциальная энергия взаимодействия двух точечных зарядов Q и q, находящихся на расстоянии r друг от друга, равна:

U = k Q q / r

(3)

Потенциальная энергия является не очень удобной характеристикой поля, так как она зависит не только от самого поля, но и от величины помещенного в поле пробного заряда. Удобнее ввести другую характеристику, равную отношению потенциальной энергии, которой обладает пробный заряд в поле, к величине этого пробного заряда: $ϕ = U / q$ . Эта величина называется потенциалом электростатического поля. Тогда работа по перемещению заряда (формула (2)) перепишется:

A_{12} = q (ϕ_{1} - ϕ_{2})

(4)

Из этой формулы ясен физический смысл потенциала. Потенциалом поля в какой-либо точке следует назвать работу, совершенную силами поля при перемещении единичного положительного точечного заряда из этой точки в ту, которая имеет нулевой потенциал.

Потенциал, как и потенциальная энергия, определяется с точностью до сложения с произвольной константой, так как непосредственным физическим смыслом обладает не сама потенциальная энергия, а работа, равная разности потенциальных энергий. Этот произвол обычно выражается в виде произвола в выборе той точки, в которой потенциал полагается равным нулю. Если создающие поле тела имеют конечные размеры и занимают конечную область пространства, то потенциал удобно считать равным нулю на бесконечно большом расстоянии от этих тел.

Из формулы (3) следует, что потенциал поля точечного заряда равен

ϕ = k Q / r

(5)

Потенциал поля, созданного произвольным распределением заряда, по принципу суперпозиции равен алгебраической сумме потенциалов полей, созданных точечными зарядами, на которые можно разбить заряженное тело.

Для графического изображения полей наряду с силовыми линиями применяются эквипотенциальные поверхности. Они представляют собой геометрическое место точек с одинаковым значением потенциала. Например, из формулы (5) видно, что эквипотенциальные поверхности поля точечного заряда представляют собой сферы, центр которых расположен в точке, в которой находится заряд.

Рис. 2

Эквипотенциальные поверхности не пересекаются. Они перпендикулярны силовым линиям. Это следует из того, что согласно (4) работа при перемещении заряда по эквипотенциальной поверхности равна нулю, в то время как действующая на заряд сила и сонаправленная с ней напряженность поля в общем случае отличны от нуля. Таким образом, вектор напряженности поля перпендикулярен любой линии на эквипотенциальной поверхности, т.е. нормален и самой поверхности.

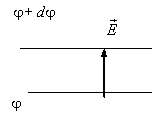
Получим связь между напряжённостью поля и потенциалом. Рассмотрим две эквипотенциальные поверхности: j = const и φ+dφ=const и будем перемещать заряд q с одной поверхности на другую по кратчайшему пути. При этом силы поля совершают работу $A = q [φ - (φ + d φ)] = - q d φ$ . С другой стороны, эта работа равна $A = F d l = q E d l$ , т.е. равна произведению силы на величину перемещения. Сравнивая два выражения для работы, получим связь между напряженностью поля и потенциалом:

E = - \frac{d φ}{d l}

(6)

Вектор напряженности поля перпендикулярен поверхности постоянного значения потенциала и направлен в сторону его наибыстрейшего убывания.

Рис. 3

Кадр из компьютерного эксперимента приведен на рис. 3. Кружочки, изображающие заряженные тела, расставляются на предназначенном для этого поле произвольным образом, им приписываются какая-либо величина и знак заряда. После этого, перемещая мышку, находят точки, имеющие заданное значение потенциала, для чего используется виртуальный гальванометр (в левой верхней части экрана).

1. Расставить заряды и присвоить им величину и знак.

Нажать кнопку «ввести», при этом станет видимой панель расстановки зарядов. Выбрать при помощи радиокнопки заряд, при помощи мышки установить его в нужную точку рабочего поля. Ввести величину и знак этого заряда. Закончив расстановку, нажать кнопку «ввод закончен».

2. При помощи ползунка установить значение потенциала Р, равное нулю.

3. Построить соответствующую эквипотенциальную линию.

Перемещая мышку по рабочему полю, найти точки, в которых потенциал равен заданному значению Р. Отклонение стрелки прибора при этом минимально, и одно из окон окрашивается в красный цвет. Нажав левую точку мышки, получите точку на рабочем поле. Таким образом можно построить всю эквипотенциальную линию.

4. Построить следующую эквипотенциальную линию.

При помощи палитры на панели управления выберите цвет эквипотенциальной линии.

Установите новое значение потенциала Ри снимите по точкам новую эквипотенциальную линию.

Распечатка программы данного компьютерного эксперимента приведена в приложении.