В условиях отсутствия последействия и аддитивности целевой функции решение задачи динамического программирования базируется на принципе оптимальности Беллмана: Метод решения задачи (2.9.1), основанный на принципе оптимальности Беллмана, называется методом прогонки и представляет собой следующую двухэтапную процедуру.

1-й этап («обратная прогонка»). Рассмотрим последний, n-й шаг. Обозначим через W_n^*(S) максимальную эффективность управления x_n на последнем шаге при условии, что в начале шага система находилась в состоянии S_n-1:

(2.9.4)

По сути, x_n^* – это условное оптимальное управление на n-м шаге:

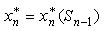(2.9.5)

Перебирая все возможные состояния S_n-1 перед последним шагом, получаем все условные оптимальные уравнения на последнем шаге.

Рассмотрим произвольный k-й шаг. Из принципа оптимальности Беллмана следует

$$W_k^{\ast }(S_{k-1})=\underset{x_k,x_{k+1},\dots ,x_n}{\max }\{f_k(S_{k-1},x_k)+{\displaystyle \sum _{i=k+1}^n{f}_i(S_{i-1},x_i)}\}=\underset{x_k}{\max }\{f_k(S_{k-1},x_k)+W_{k+1}^{\ast }(S_k)\}=$$$$=\underset{x_k}{\max }\{f_k(S_{k-1},x_k)+W_{k+1}^{\ast }({\varphi }_k(S_{k-1},x_k))\},k=\overline{\text{1}\text{,}n}.$$

(2.9.6)

Уравнения (2.9.6) называются рекуррентными уравнениями Беллмана и позволяют находить цепочки условных оптимальных шаговых управлений, от последнего $x_n$

и до самого первого $x_1$:

$$x_n^{\ast }(S_{n-1}),x_{n-1}^{\ast }(S_{n-2}),\dots ,x_k^{\ast }(S_{k-1}),\dots ,x_1^{\ast }(S_0).$$

(2.9.7)