Пусть случайный процесс ξ(t) изменения во времени состояний некоторой системы принимает целочисленные значения i=1,2,… из множества X конечного или счетного, то есть ξ(t)=i, ξ(t´)=j. Переходы из одного состояния в другое происходят через равные промежутки времени |t–t´|=1, которые будем называть шагом.

Условные вероятности P{ξ(t´)=j|ξ(t)=i}=p_ij(t) для всех i,j∈X образуют матрицу вероятностей переходов цепи Маркова из одного состояния в другое в момент времени t.

Если вероятности переходов не зависят от момента времени t, то есть p_ij(t)=p_ij, то цепь Маркова называется однородной с матрицей вероятностей переходов за один шаг

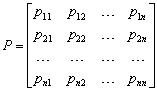где n – число состояний системы (число возможных значений цепи Маркова) – конечное или счетное. Элементы матрицы p_ij >0 и удовлетворяют условию нормировки

, .

 

Такую матрицу называют стохастической или марковской.

Набор вероятностей , где называется начальным распределением, оно определяет состояние системы в начальный момент времени.

Цепь Маркова с дискретным временем полностью определяется матрицей вероятностей переходов за один шаг и начальным распределением.

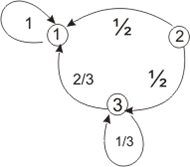
Для описания цепи Маркова удобно использовать граф вероятностей переходов, вершины которого обозначают возможные состояния системы, стрелки от одной вершины к другой указывают возможные переходы между состояниями, а число над стрелкой задаёт вероятность такого перехода. Например, пусть множество состояний X={1,2,3}, матрица вероятностей переходов имеет вид

,

 

тогда граф вероятностей переходов выглядит следующим образом:

 

В дополнение к одношаговым вероятностям переходов интересно рассмотреть вероятности переходов из одного состояния в другое за произвольное число шагов. В силу уравнения Чепмена–Колмогорова для цепей Маркова, то есть для марковских процессов с дискретным множеством состояний, эти вероятности удовлетворяют рекуррентным соотношениям

, (2.2)

 

которые нетрудно получить, применяя формулу полной вероятности.

Обозначим через A событие, заключающееся в том, что система за (n+1) шагов перейдёт из состояния i в состояние j, через H_k – событие, состоящее в том, что за n шагов система перейдёт из состояния i в состояние k, тогда в силу формулы полной вероятности

,

 

обозначив

, , ,

 

можно записать равенство, совпадающее с (2.2).

Совершенно аналогично, можно получить уравнение Чепмена–Колмогорова для произвольного числа шагов n+μ в виде

, (2.3)

 

которое позволяет определять вероятности переходов из одного состояния в другое за произвольное число шагов. Этими формулами удобнее пользоваться, записав их в матричном виде. Так, равенство (2.2) при n=1 в матричной форме имеет вид

,

тогда равенство (2.3) примет вид

.

Заметим, что матрицы Π(n) тоже стохастические ∀n.

Для распределения вероятностей состояний однородной цепи Маркова имеет место следующее равенство векторов:

.

Для неоднородной цепи Маркова распределение вероятностей находится по формулам

.