Основным объектом многомерного анализа является таблица "объект – признак". Все признаки можно считать количественными. Каждый признак отображается на числовую ось и отражает расстояние между объектами. Каждый признак имеет определенный вес, характеризующий относительную важность этого признака и равный его дисперсии. После стандартной нормировки на среднеквадратичное отклонение все признаки имеют равный вес. Веса объектов считаются равными. Более сложную ситуацию, когда объектам тоже приписываются разные веса, рассматривать не будем. Отметим только, что она не сводится ни к случаю еще одного признака, ни к умножению значений объектов на веса.

Введем следующие определения:

Скаляр – действительное число.

Вектор – набор скаляров.

Матрица – набор векторов одинаковой длины.

Вектор-строка – матрица из одной строки.

Вектор-столбец – матрица из одного столбца.

Операции:

Умножение матрицы на скаляр.

Cкалярное произведение векторов 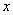 и : 

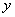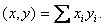
Умножение матрицы на вектор.

Умножение матрицы на матрицу.

Сложение матриц.

Транспонирование матрицы. .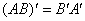

Единичная матрица 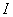.   Диагональная матрица .

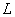Ортогональная матрица .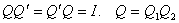

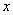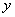
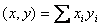Будем считать известными понятия скаляра, вектора, матрицы (единичная, диагональная, ортогональная) и операций над ними: умножение матрицы на скаляр, скалярное произведение векторов  и  , умножение матрицы на вектор, умножение матрицы на матрицу, сложение матриц, транспонирование матрицы (Ланкастер, 1978).

Таблица "объект – признак" является матрицей, а каждый объект – вектором. Каждый признак тоже является вектором. Геометрическое представление: если в качестве осей выбрать признаки, то каждый объект может быть представлен точкой в этом пространстве. Координатами точки служат значения признаков. Такое пространство будем называть пространством объектов или основным. Если в качестве осей выбрать объекты, то каждый признак может быть представлен точкой в этом пространстве. Будем называть его пространством признаков или двойственным. Оба пространства определены одновременно на основе одной и той же матрицы. Если значения в матрице меняются, то одновременно меняются положения объектов и признаков, как точек в соответствующих пространствах.

Размерность – важнейшее свойство пространства. Размерность основного пространства – число признаков. Размерность двойственного – число объектов. Если размерность равна единице, то точки можно расположить на числовой оси. Если размерность равна двум, то их можно расположить на плоскости. Если размерность равна трем, то совокупность точек еще можно представить наглядно в привычном для наших органов чувств виде, разместив их в пространстве. Если размерность пространства больше трех, то взаимное расположение точек в этом пространстве можно представить только мысленно, хотя и существуют различные хитроумные приемы для визуального отображения пространств большей размерности: физико-географические карты (цвет), полигоны, лица Чернова и т.д.

Определим в пространстве расстояние между точками по формуле 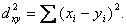 Такое расстояние является многомерным обобщением обычного пифагорова расстояния и называется евклидовым. Евклидовым называется и все пространство, если в нем определено евклидово расстояние. Каждую точку можно рассматривать как вектор относительно начала координат.

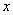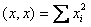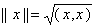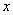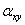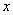Вычислим скалярное произведение вектора  само на себя . Показатель называется длиной вектора и является расстоянием до точки  от начала координат. Определим угол  между  и 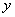 по формуле 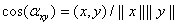. Показатель  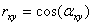называется коэффициентом корреляции между признаками.