Сложное напряженное состояние равноопасно с простым растяжением, если эти напряженные состояния имеют одинаковые удельные энергии изменения формы.
В общем случае деформации часть энергии деформации ЕpV расходуется на изменение объема, а другая часть энергии Epf — на изменение формы тела:
Ep = EpV+Epf. |
(8) |
Это равносильно представлению заданного напряженного состояния в виде суммы двух состояний. Первое соответствует гидростатическому растяжению (сжатию), при котором на всех гранях элементарного объема действуют одинаковые средние напряжения
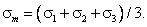 |
(9) |
Под действием этих напряжений форма элементарного объема не меняется, а изменяется лишь его объем за счет одинакового удлинения (укорочения) длин всех ребер. При объемном напряженном состоянии в главных напряжениях:
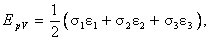
где σ1, σ2, σ3 и ε1, ε2, ε2 – главные напряжения и деформации.
Подставив закон Гука, получим:
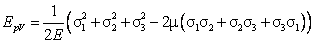 |
(10) |
Подставив соотношение (9) в формулу (10) вместо σ1, σ2 и σ3, найдем:
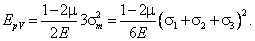 |
(11) |
Второе напряженное состояние с компонентами напряжений на гранях элементарного объема: 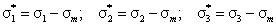 изменяет лишь форму тела. Потенциальная энергия изменения формы тела:
изменяет лишь форму тела. Потенциальная энергия изменения формы тела:
Epf=Ep – EpV .
Из этого уравнения с учетом формул (10) и (11) получим:
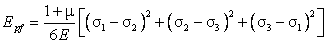 . . |
(12) |
Для простого растяжения (σ1= σэкв; σ2 = σ3 = 0) из формулы (12) будем иметь:
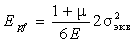 |
(13) |
Сравнивая равенства (12) и (13), устанавливаем:
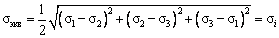 , , |
(14) |
σi называют интенсивностью напряжений
Для плоского напряженного состояния соотношение (14) принимает вид:
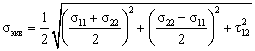 . . |
(15) |
Если σ22=0, то положив σ11 = σ, τ12 = τ, получим:
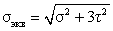 . . |
(16) |
Эта теория предложена в начале XX в. Губером и Мизесом. Она хорошо согласуется с экспериментами для пластичных материалов и широко применяется на практике.
Соотношения (13)÷(16) используют в качестве условий пластичности, определяя условия возникновения пластических деформаций в материале:
σэкв = σт .
При чистом сдвиге σ = 0, τ = τт из формулы (16) получим предел текучести:
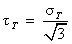 .
.
В отличие от этого результата, по третьей теории прочности в случае чистого сдвига (см. формулу (7) для σ11 = σ22=0, τ12 = τ, σэкв = σт) получим 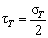 .
.
Отметим, что описанная теория предсказывает одинаковую прочность при растяжении и сжатии, так как эквивалентные напряжения в обоих случаях одинаковы.